Assignment 2#

Question 1#

%pip install pytensor pymc

Requirement already satisfied: pytensor in /usr/local/lib/python3.10/dist-packages (2.14.2)
Requirement already satisfied: pymc in /usr/local/lib/python3.10/dist-packages (5.7.2)
Requirement already satisfied: setuptools>=48.0.0 in /usr/local/lib/python3.10/dist-packages (from pytensor) (67.7.2)
Requirement already satisfied: scipy>=0.14 in /usr/local/lib/python3.10/dist-packages (from pytensor) (1.11.4)
Requirement already satisfied: numpy>=1.17.0 in /usr/local/lib/python3.10/dist-packages (from pytensor) (1.25.2)
Requirement already satisfied: filelock in /usr/local/lib/python3.10/dist-packages (from pytensor) (3.13.1)
Requirement already satisfied: etuples in /usr/local/lib/python3.10/dist-packages (from pytensor) (0.3.9)
Requirement already satisfied: logical-unification in /usr/local/lib/python3.10/dist-packages (from pytensor) (0.4.6)
Requirement already satisfied: miniKanren in /usr/local/lib/python3.10/dist-packages (from pytensor) (1.0.3)
Requirement already satisfied: cons in /usr/local/lib/python3.10/dist-packages (from pytensor) (0.4.6)
Requirement already satisfied: typing-extensions in /usr/local/lib/python3.10/dist-packages (from pytensor) (4.9.0)
Requirement already satisfied: arviz>=0.13.0 in /usr/local/lib/python3.10/dist-packages (from pymc) (0.15.1)
Requirement already satisfied: cachetools>=4.2.1 in /usr/local/lib/python3.10/dist-packages (from pymc) (5.3.2)
Requirement already satisfied: cloudpickle in /usr/local/lib/python3.10/dist-packages (from pymc) (2.2.1)
Requirement already satisfied: fastprogress>=0.2.0 in /usr/local/lib/python3.10/dist-packages (from pymc) (1.0.3)
Requirement already satisfied: pandas>=0.24.0 in /usr/local/lib/python3.10/dist-packages (from pymc) (1.5.3)
Requirement already satisfied: matplotlib>=3.2 in /usr/local/lib/python3.10/dist-packages (from arviz>=0.13.0->pymc) (3.7.1)
Requirement already satisfied: packaging in /usr/local/lib/python3.10/dist-packages (from arviz>=0.13.0->pymc) (23.2)
Requirement already satisfied: xarray>=0.21.0 in /usr/local/lib/python3.10/dist-packages (from arviz>=0.13.0->pymc) (2023.7.0)
Requirement already satisfied: h5netcdf>=1.0.2 in /usr/local/lib/python3.10/dist-packages (from arviz>=0.13.0->pymc) (1.3.0)
Requirement already satisfied: xarray-einstats>=0.3 in /usr/local/lib/python3.10/dist-packages (from arviz>=0.13.0->pymc) (0.7.0)
Requirement already satisfied: python-dateutil>=2.8.1 in /usr/local/lib/python3.10/dist-packages (from pandas>=0.24.0->pymc) (2.8.2)
Requirement already satisfied: pytz>=2020.1 in /usr/local/lib/python3.10/dist-packages (from pandas>=0.24.0->pymc) (2023.4)
Requirement already satisfied: toolz in /usr/local/lib/python3.10/dist-packages (from logical-unification->pytensor) (0.12.1)
Requirement already satisfied: multipledispatch in /usr/local/lib/python3.10/dist-packages (from logical-unification->pytensor) (1.0.0)
Requirement already satisfied: h5py in /usr/local/lib/python3.10/dist-packages (from h5netcdf>=1.0.2->arviz>=0.13.0->pymc) (3.9.0)
Requirement already satisfied: contourpy>=1.0.1 in /usr/local/lib/python3.10/dist-packages (from matplotlib>=3.2->arviz>=0.13.0->pymc) (1.2.0)
Requirement already satisfied: cycler>=0.10 in /usr/local/lib/python3.10/dist-packages (from matplotlib>=3.2->arviz>=0.13.0->pymc) (0.12.1)
Requirement already satisfied: fonttools>=4.22.0 in /usr/local/lib/python3.10/dist-packages (from matplotlib>=3.2->arviz>=0.13.0->pymc) (4.49.0)
Requirement already satisfied: kiwisolver>=1.0.1 in /usr/local/lib/python3.10/dist-packages (from matplotlib>=3.2->arviz>=0.13.0->pymc) (1.4.5)
Requirement already satisfied: pillow>=6.2.0 in /usr/local/lib/python3.10/dist-packages (from matplotlib>=3.2->arviz>=0.13.0->pymc) (9.4.0)
Requirement already satisfied: pyparsing>=2.3.1 in /usr/local/lib/python3.10/dist-packages (from matplotlib>=3.2->arviz>=0.13.0->pymc) (3.1.1)
Requirement already satisfied: six>=1.5 in /usr/local/lib/python3.10/dist-packages (from python-dateutil>=2.8.1->pandas>=0.24.0->pymc) (1.16.0)

from sklearn.datasets import load_breast_cancer
cancer1 = load_breast_cancer()

print("Predictors: ", cancer1.feature_names)

Predictors:  ['mean radius' 'mean texture' 'mean perimeter' 'mean area'
 'mean smoothness' 'mean compactness' 'mean concavity'
 'mean concave points' 'mean symmetry' 'mean fractal dimension'
 'radius error' 'texture error' 'perimeter error' 'area error'
 'smoothness error' 'compactness error' 'concavity error'
 'concave points error' 'symmetry error' 'fractal dimension error'
 'worst radius' 'worst texture' 'worst perimeter' 'worst area'
 'worst smoothness' 'worst compactness' 'worst concavity'
 'worst concave points' 'worst symmetry' 'worst fractal dimension']

import pandas as pd

cancer = pd.DataFrame(cancer1.data, columns=cancer1.feature_names)
cancer.columns = cancer.columns.str.replace(' ','_')

cancer.shape

(569, 30)

cancer

	mean_radius	mean_texture	mean_perimeter	mean_area	mean_smoothness	mean_compactness	mean_concavity	mean_concave_points	mean_symmetry	mean_fractal_dimension	...	worst_radius	worst_texture	worst_perimeter	worst_area	worst_smoothness	worst_compactness	worst_concavity	worst_concave_points	worst_symmetry	worst_fractal_dimension
0	17.99	10.38	122.80	1001.0	0.11840	0.27760	0.30010	0.14710	0.2419	0.07871	...	25.380	17.33	184.60	2019.0	0.16220	0.66560	0.7119	0.2654	0.4601	0.11890
1	20.57	17.77	132.90	1326.0	0.08474	0.07864	0.08690	0.07017	0.1812	0.05667	...	24.990	23.41	158.80	1956.0	0.12380	0.18660	0.2416	0.1860	0.2750	0.08902
2	19.69	21.25	130.00	1203.0	0.10960	0.15990	0.19740	0.12790	0.2069	0.05999	...	23.570	25.53	152.50	1709.0	0.14440	0.42450	0.4504	0.2430	0.3613	0.08758
3	11.42	20.38	77.58	386.1	0.14250	0.28390	0.24140	0.10520	0.2597	0.09744	...	14.910	26.50	98.87	567.7	0.20980	0.86630	0.6869	0.2575	0.6638	0.17300
4	20.29	14.34	135.10	1297.0	0.10030	0.13280	0.19800	0.10430	0.1809	0.05883	...	22.540	16.67	152.20	1575.0	0.13740	0.20500	0.4000	0.1625	0.2364	0.07678
...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...
564	21.56	22.39	142.00	1479.0	0.11100	0.11590	0.24390	0.13890	0.1726	0.05623	...	25.450	26.40	166.10	2027.0	0.14100	0.21130	0.4107	0.2216	0.2060	0.07115
565	20.13	28.25	131.20	1261.0	0.09780	0.10340	0.14400	0.09791	0.1752	0.05533	...	23.690	38.25	155.00	1731.0	0.11660	0.19220	0.3215	0.1628	0.2572	0.06637
566	16.60	28.08	108.30	858.1	0.08455	0.10230	0.09251	0.05302	0.1590	0.05648	...	18.980	34.12	126.70	1124.0	0.11390	0.30940	0.3403	0.1418	0.2218	0.07820
567	20.60	29.33	140.10	1265.0	0.11780	0.27700	0.35140	0.15200	0.2397	0.07016	...	25.740	39.42	184.60	1821.0	0.16500	0.86810	0.9387	0.2650	0.4087	0.12400
568	7.76	24.54	47.92	181.0	0.05263	0.04362	0.00000	0.00000	0.1587	0.05884	...	9.456	30.37	59.16	268.6	0.08996	0.06444	0.0000	0.0000	0.2871	0.07039

569 rows × 30 columns

# Add a column for the response variable: malignant or benign
cancer['Target'] = cancer1.target

cancer

	mean_radius	mean_texture	mean_perimeter	mean_area	mean_smoothness	mean_compactness	mean_concavity	mean_concave_points	mean_symmetry	mean_fractal_dimension	...	worst_texture	worst_perimeter	worst_area	worst_smoothness	worst_compactness	worst_concavity	worst_concave_points	worst_symmetry	worst_fractal_dimension	Target
0	17.99	10.38	122.80	1001.0	0.11840	0.27760	0.30010	0.14710	0.2419	0.07871	...	17.33	184.60	2019.0	0.16220	0.66560	0.7119	0.2654	0.4601	0.11890	0
1	20.57	17.77	132.90	1326.0	0.08474	0.07864	0.08690	0.07017	0.1812	0.05667	...	23.41	158.80	1956.0	0.12380	0.18660	0.2416	0.1860	0.2750	0.08902	0
2	19.69	21.25	130.00	1203.0	0.10960	0.15990	0.19740	0.12790	0.2069	0.05999	...	25.53	152.50	1709.0	0.14440	0.42450	0.4504	0.2430	0.3613	0.08758	0
3	11.42	20.38	77.58	386.1	0.14250	0.28390	0.24140	0.10520	0.2597	0.09744	...	26.50	98.87	567.7	0.20980	0.86630	0.6869	0.2575	0.6638	0.17300	0
4	20.29	14.34	135.10	1297.0	0.10030	0.13280	0.19800	0.10430	0.1809	0.05883	...	16.67	152.20	1575.0	0.13740	0.20500	0.4000	0.1625	0.2364	0.07678	0
...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...
564	21.56	22.39	142.00	1479.0	0.11100	0.11590	0.24390	0.13890	0.1726	0.05623	...	26.40	166.10	2027.0	0.14100	0.21130	0.4107	0.2216	0.2060	0.07115	0
565	20.13	28.25	131.20	1261.0	0.09780	0.10340	0.14400	0.09791	0.1752	0.05533	...	38.25	155.00	1731.0	0.11660	0.19220	0.3215	0.1628	0.2572	0.06637	0
566	16.60	28.08	108.30	858.1	0.08455	0.10230	0.09251	0.05302	0.1590	0.05648	...	34.12	126.70	1124.0	0.11390	0.30940	0.3403	0.1418	0.2218	0.07820	0
567	20.60	29.33	140.10	1265.0	0.11780	0.27700	0.35140	0.15200	0.2397	0.07016	...	39.42	184.60	1821.0	0.16500	0.86810	0.9387	0.2650	0.4087	0.12400	0
568	7.76	24.54	47.92	181.0	0.05263	0.04362	0.00000	0.00000	0.1587	0.05884	...	30.37	59.16	268.6	0.08996	0.06444	0.0000	0.0000	0.2871	0.07039	1

569 rows × 31 columns

cancer.shape

(569, 31)

Next, we will split up our predictor and response data into training datasets and testing datasets. Recall, we will use the training dataset to train our logistic regression models and then use the testing dataset to test the accuracy of model predictions. There is a nice function from sklearn.model_selection called train_test_split that splits a given dataset into 75% training and 25% testing data. Stetting random_state=123 allows you to generate the same random train and test subsets used in this article. It’s not strictly necessary to split data into training and testing sets when performing logistic regression. In fact if you have limited data it’s not wise to do. However, we do it in this article to demonstrate how each method leads to the same results. For the logistic regression examples, we will model malignant or benign as a function of the first 10 predictors (columns) in our dataset. These first 10 correspond to mean measurements of each tumor; mean radius, mean texture, mean perimeter, mean area, etc. (We selected these 10 columns purely for convenience to limit output. The goal of this article is to present different ways of performing logistic regression in Python, not how to select variables.)

from sklearn.model_selection import train_test_split

# Select the first 10 columns of our DataFrame that we will use as the predictors in our models
x = cancer.iloc[:,:10]

# Select the response column
y = cancer.Target


from sklearn.model_selection import train_test_split

# Split these data into training and testing datasets
x_train, x_test, y_train, y_test = train_test_split(x,y, random_state=123)

# Create a new DataFrame by concatenating x and y
new_dataset = pd.concat([x, y], axis=1)

new_dataset

	mean_radius	mean_texture	mean_perimeter	mean_area	mean_smoothness	mean_compactness	mean_concavity	mean_concave_points	mean_symmetry	mean_fractal_dimension	Target
0	17.99	10.38	122.80	1001.0	0.11840	0.27760	0.30010	0.14710	0.2419	0.07871	0
1	20.57	17.77	132.90	1326.0	0.08474	0.07864	0.08690	0.07017	0.1812	0.05667	0
2	19.69	21.25	130.00	1203.0	0.10960	0.15990	0.19740	0.12790	0.2069	0.05999	0
3	11.42	20.38	77.58	386.1	0.14250	0.28390	0.24140	0.10520	0.2597	0.09744	0
4	20.29	14.34	135.10	1297.0	0.10030	0.13280	0.19800	0.10430	0.1809	0.05883	0
...	...	...	...	...	...	...	...	...	...	...	...
564	21.56	22.39	142.00	1479.0	0.11100	0.11590	0.24390	0.13890	0.1726	0.05623	0
565	20.13	28.25	131.20	1261.0	0.09780	0.10340	0.14400	0.09791	0.1752	0.05533	0
566	16.60	28.08	108.30	858.1	0.08455	0.10230	0.09251	0.05302	0.1590	0.05648	0
567	20.60	29.33	140.10	1265.0	0.11780	0.27700	0.35140	0.15200	0.2397	0.07016	0
568	7.76	24.54	47.92	181.0	0.05263	0.04362	0.00000	0.00000	0.1587	0.05884	1

569 rows × 11 columns

#using stripplot function from seaborn
import seaborn as sns

sns.pairplot(new_dataset, hue='Target', diag_kind='kde', height=1.5)

import numpy as np

xv_train = x_train.values
xv_test = x_test.values
shape_xv = np.shape(xv_train)
yv_train = y_train.values
yv_test = y_test.values

print(np.shape(xv_train))
print(np.shape(xv_test))
print(np.shape(yv_train))
print(np.shape(yv_test))

(426, 10)
(143, 10)
(426,)
(143,)

Building the model#

import pymc as pm

with pm.Model() as model_1:

    α = pm.Normal('α', mu=0, sigma=5)
    β = pm.Normal('β', mu=0, sigma=5, shape=shape_xv[1])

    μ = α + pm.math.dot(xv_train, β)

    θ = pm.Deterministic('θ', 1 / (1 + pm.math.exp(-μ)))
    #bd = pm.Deterministic('bd', -α/β[1] - β[0]/β[1] * x_1[:,0])

    yl = pm.Bernoulli('yl', p=θ, observed=yv_train)

    trace_1 = pm.sample(1000, tune=2000, return_inferencedata=True, target_accept=0.85)

100.00% [3000/3000 05:14<00:00 Sampling chain 0, 0 divergences]

100.00% [3000/3000 05:16<00:00 Sampling chain 1, 0 divergences]

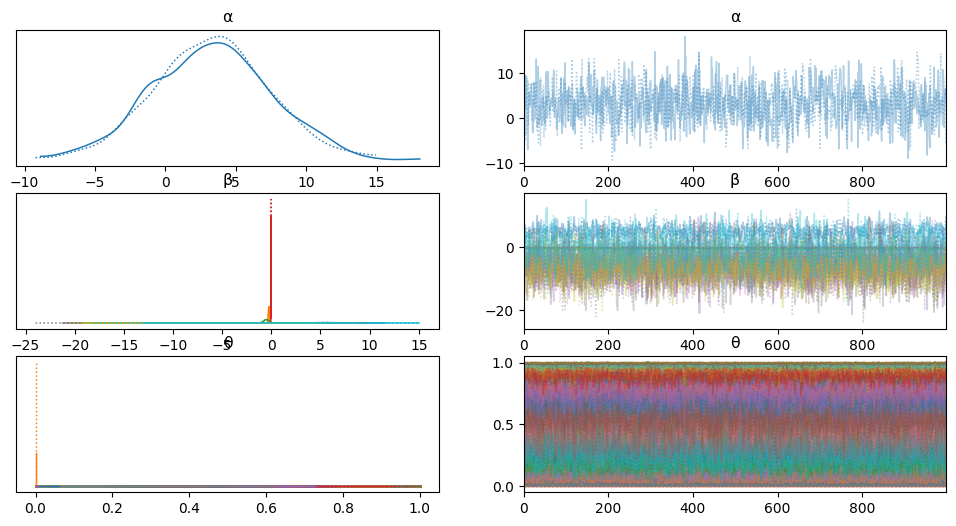
import arviz as az

az.plot_trace(trace_1)

array([[<Axes: title={'center': 'α'}>, <Axes: title={'center': 'α'}>],
       [<Axes: title={'center': 'β'}>, <Axes: title={'center': 'β'}>],
       [<Axes: title={'center': 'θ'}>, <Axes: title={'center': 'θ'}>]],
      dtype=object)

az.summary(trace_1)

	mean	sd	hdi_3%	hdi_97%	mcse_mean	mcse_sd	ess_bulk	ess_tail	r_hat
α	3.265	4.098	-3.902	11.622	0.122	0.089	1128.0	1242.0	1.0
β[0]	5.155	1.751	1.874	8.353	0.058	0.041	931.0	1165.0	1.0
β[1]	-0.258	0.053	-0.359	-0.164	0.001	0.001	2018.0	1436.0	1.0
β[2]	-0.527	0.242	-0.977	-0.082	0.008	0.005	1052.0	1034.0	1.0
β[3]	-0.030	0.008	-0.044	-0.016	0.000	0.000	1170.0	1115.0	1.0
...	...	...	...	...	...	...	...	...	...
θ[421]	0.996	0.003	0.992	1.000	0.000	0.000	2022.0	1260.0	1.0
θ[422]	0.990	0.006	0.980	0.998	0.000	0.000	1886.0	1418.0	1.0
θ[423]	0.896	0.042	0.820	0.969	0.001	0.001	1886.0	1643.0	1.0
θ[424]	0.000	0.000	0.000	0.001	0.000	0.000	1424.0	1466.0	1.0
θ[425]	0.988	0.006	0.976	0.997	0.000	0.000	2123.0	1659.0	1.0

437 rows × 9 columns

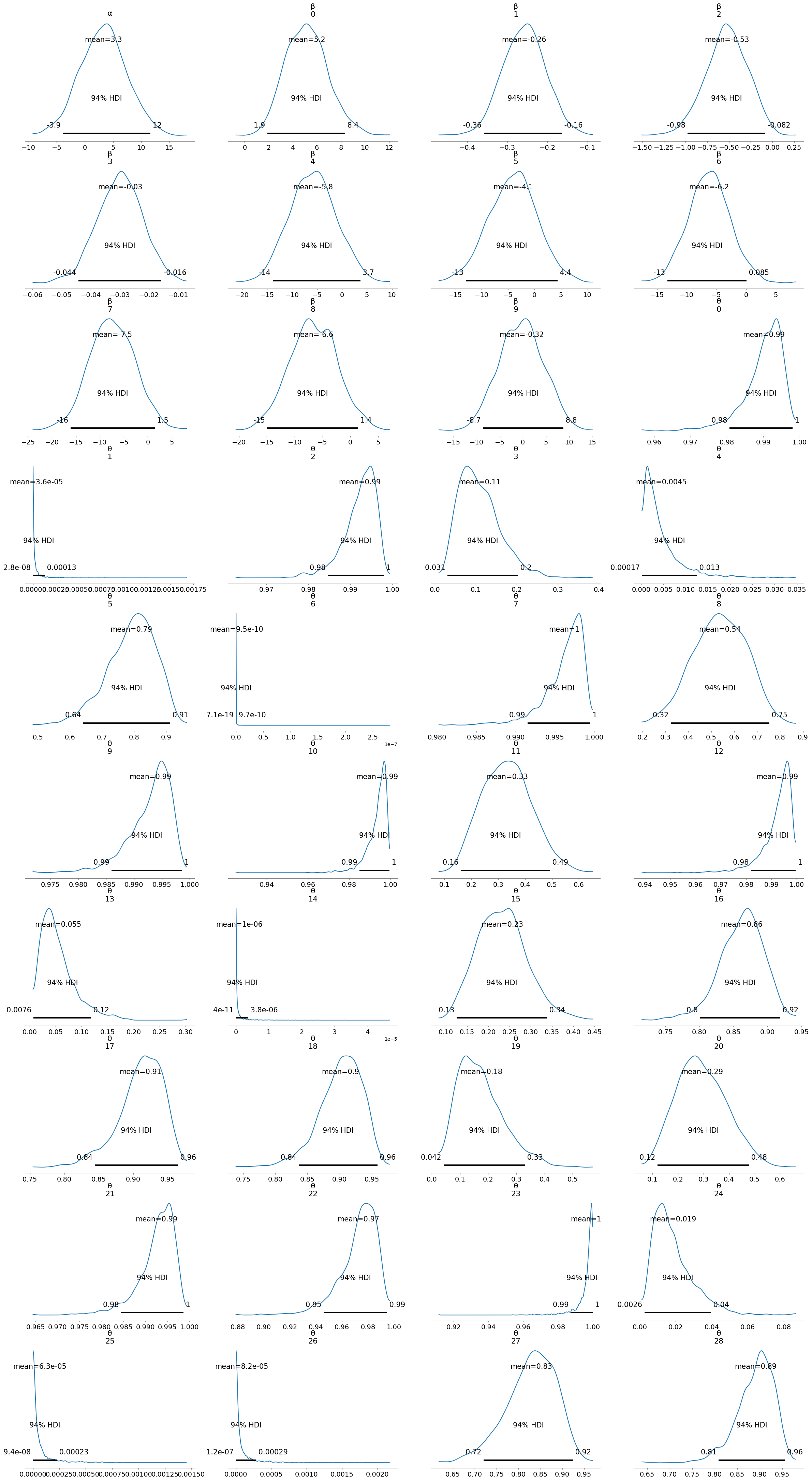
az.plot_posterior(trace_1)

/usr/local/lib/python3.10/dist-packages/arviz/plots/plot_utils.py:271: UserWarning: rcParams['plot.max_subplots'] (40) is smaller than the number of variables to plot (437) in plot_posterior, generating only 40 plots
  warnings.warn(

array([[<Axes: title={'center': 'α'}>, <Axes: title={'center': 'β\n0'}>,
        <Axes: title={'center': 'β\n1'}>,
        <Axes: title={'center': 'β\n2'}>],
       [<Axes: title={'center': 'β\n3'}>,
        <Axes: title={'center': 'β\n4'}>,
        <Axes: title={'center': 'β\n5'}>,
        <Axes: title={'center': 'β\n6'}>],
       [<Axes: title={'center': 'β\n7'}>,
        <Axes: title={'center': 'β\n8'}>,
        <Axes: title={'center': 'β\n9'}>,
        <Axes: title={'center': 'θ\n0'}>],
       [<Axes: title={'center': 'θ\n1'}>,
        <Axes: title={'center': 'θ\n2'}>,
        <Axes: title={'center': 'θ\n3'}>,
        <Axes: title={'center': 'θ\n4'}>],
       [<Axes: title={'center': 'θ\n5'}>,
        <Axes: title={'center': 'θ\n6'}>,
        <Axes: title={'center': 'θ\n7'}>,
        <Axes: title={'center': 'θ\n8'}>],
       [<Axes: title={'center': 'θ\n9'}>,
        <Axes: title={'center': 'θ\n10'}>,
        <Axes: title={'center': 'θ\n11'}>,
        <Axes: title={'center': 'θ\n12'}>],
       [<Axes: title={'center': 'θ\n13'}>,
        <Axes: title={'center': 'θ\n14'}>,
        <Axes: title={'center': 'θ\n15'}>,
        <Axes: title={'center': 'θ\n16'}>],
       [<Axes: title={'center': 'θ\n17'}>,
        <Axes: title={'center': 'θ\n18'}>,
        <Axes: title={'center': 'θ\n19'}>,
        <Axes: title={'center': 'θ\n20'}>],
       [<Axes: title={'center': 'θ\n21'}>,
        <Axes: title={'center': 'θ\n22'}>,
        <Axes: title={'center': 'θ\n23'}>,
        <Axes: title={'center': 'θ\n24'}>],
       [<Axes: title={'center': 'θ\n25'}>,
        <Axes: title={'center': 'θ\n26'}>,
        <Axes: title={'center': 'θ\n27'}>,
        <Axes: title={'center': 'θ\n28'}>]], dtype=object)

Predictions on test data#

alpha_chain = trace_1.posterior['α'].mean(axis=0).values
beta_chain  = trace_1.posterior['β'].mean(axis=0).values

print(np.shape(alpha_chain), np.shape(beta_chain))

(1000,) (1000, 10)

logit = np.dot(xv_test, beta_chain.T) + alpha_chain
print(np.shape(logit))

(143, 1000)

probabilities = 1 / (1 + np.exp(-logit))
print(np.shape(probabilities))

(143, 1000)

np.shape(yv_test)

(143,)

# Average probabilities for prediction
mean_probabilities = np.mean(probabilities, axis=1)

# Class assignment (you might adjust the threshold if needed, default is 0.5)
class_assignments = (mean_probabilities > 0.5).astype(int)

# Uncertainty estimation
lower_bound = np.percentile(probabilities, 2.5, axis=1)
upper_bound = np.percentile(probabilities, 97.5, axis=1)

print("\n=======================================")
print("TEST DATA: \n", xv_test.T)
print("=======================================\n")
print("class, probabilities, ranges(94%HDI): ")
for g,h,i,j,k in zip(yv_test, class_assignments, mean_probabilities, lower_bound,upper_bound):
  print(f"ground-truth: {g}, class: {h}, mean prob. {i:.4f}, 94% HDI: [{j:.4f},{k:.4f}]")

print("=======================================\n")

=======================================
TEST DATA: 
 [[1.125e+01 9.742e+00 1.754e+01 ... 2.055e+01 1.287e+01 2.321e+01]
 [1.478e+01 1.567e+01 1.932e+01 ... 2.086e+01 1.954e+01 2.697e+01]
 [7.138e+01 6.150e+01 1.151e+02 ... 1.378e+02 8.267e+01 1.535e+02]
 ...
 [2.941e-03 1.407e-02 7.488e-02 ... 1.322e-01 2.090e-02 1.237e-01]
 [1.773e-01 2.081e-01 1.506e-01 ... 2.127e-01 1.861e-01 1.909e-01]
 [6.081e-02 6.312e-02 5.491e-02 ... 6.251e-02 6.347e-02 6.309e-02]]
=======================================

class, probabilities, ranges(94%HDI): 
ground-truth: 1, class: 1, mean prob. 0.9979, 94% HDI: [0.9954,0.9992]
ground-truth: 1, class: 1, mean prob. 0.9974, 94% HDI: [0.9937,0.9992]
ground-truth: 0, class: 0, mean prob. 0.0271, 94% HDI: [0.0095,0.0606]
ground-truth: 1, class: 1, mean prob. 0.9844, 94% HDI: [0.9722,0.9926]
ground-truth: 0, class: 0, mean prob. 0.0024, 94% HDI: [0.0004,0.0075]
ground-truth: 1, class: 1, mean prob. 0.6446, 94% HDI: [0.5177,0.7538]
ground-truth: 1, class: 1, mean prob. 0.9575, 94% HDI: [0.9341,0.9746]
ground-truth: 0, class: 1, mean prob. 0.9876, 94% HDI: [0.9773,0.9938]
ground-truth: 1, class: 1, mean prob. 0.9467, 94% HDI: [0.9040,0.9756]
ground-truth: 1, class: 1, mean prob. 0.9081, 94% HDI: [0.8591,0.9464]
ground-truth: 1, class: 1, mean prob. 0.9877, 94% HDI: [0.9760,0.9953]
ground-truth: 0, class: 0, mean prob. 0.0116, 94% HDI: [0.0039,0.0260]
ground-truth: 0, class: 0, mean prob. 0.0983, 94% HDI: [0.0383,0.1964]
ground-truth: 1, class: 1, mean prob. 0.9915, 94% HDI: [0.9840,0.9962]
ground-truth: 0, class: 0, mean prob. 0.0060, 94% HDI: [0.0011,0.0180]
ground-truth: 1, class: 1, mean prob. 0.9626, 94% HDI: [0.9408,0.9781]
ground-truth: 1, class: 1, mean prob. 0.9908, 94% HDI: [0.9833,0.9957]
ground-truth: 1, class: 1, mean prob. 0.9876, 94% HDI: [0.9791,0.9937]
ground-truth: 1, class: 1, mean prob. 0.9717, 94% HDI: [0.9510,0.9848]
ground-truth: 1, class: 1, mean prob. 0.9860, 94% HDI: [0.9751,0.9930]
ground-truth: 0, class: 0, mean prob. 0.0000, 94% HDI: [0.0000,0.0000]
ground-truth: 0, class: 1, mean prob. 0.9401, 94% HDI: [0.9092,0.9642]
ground-truth: 1, class: 1, mean prob. 0.9714, 94% HDI: [0.9509,0.9853]
ground-truth: 1, class: 1, mean prob. 0.9655, 94% HDI: [0.9274,0.9881]
ground-truth: 1, class: 1, mean prob. 0.9862, 94% HDI: [0.9748,0.9940]
ground-truth: 0, class: 0, mean prob. 0.0251, 94% HDI: [0.0099,0.0493]
ground-truth: 0, class: 0, mean prob. 0.0583, 94% HDI: [0.0290,0.1002]
ground-truth: 1, class: 1, mean prob. 0.9923, 94% HDI: [0.9856,0.9963]
ground-truth: 0, class: 0, mean prob. 0.1865, 94% HDI: [0.1056,0.2782]
ground-truth: 1, class: 1, mean prob. 0.9979, 94% HDI: [0.9950,0.9993]
ground-truth: 0, class: 1, mean prob. 0.7574, 94% HDI: [0.6417,0.8530]
ground-truth: 1, class: 1, mean prob. 0.9951, 94% HDI: [0.9903,0.9980]
ground-truth: 1, class: 1, mean prob. 0.9559, 94% HDI: [0.9261,0.9765]
ground-truth: 1, class: 1, mean prob. 0.9906, 94% HDI: [0.9829,0.9954]
ground-truth: 0, class: 0, mean prob. 0.3801, 94% HDI: [0.2711,0.5056]
ground-truth: 1, class: 1, mean prob. 0.9963, 94% HDI: [0.9921,0.9986]
ground-truth: 1, class: 1, mean prob. 0.9557, 94% HDI: [0.9238,0.9773]
ground-truth: 1, class: 1, mean prob. 0.9856, 94% HDI: [0.9757,0.9924]
ground-truth: 1, class: 1, mean prob. 0.9851, 94% HDI: [0.9737,0.9926]
ground-truth: 0, class: 0, mean prob. 0.0003, 94% HDI: [0.0000,0.0012]
ground-truth: 0, class: 1, mean prob. 0.5834, 94% HDI: [0.4833,0.6747]
ground-truth: 1, class: 1, mean prob. 0.9908, 94% HDI: [0.9807,0.9965]
ground-truth: 0, class: 1, mean prob. 0.5778, 94% HDI: [0.4193,0.7278]
ground-truth: 1, class: 1, mean prob. 0.9222, 94% HDI: [0.8904,0.9480]
ground-truth: 0, class: 0, mean prob. 0.1962, 94% HDI: [0.1210,0.2904]
ground-truth: 1, class: 1, mean prob. 0.9172, 94% HDI: [0.8597,0.9581]
ground-truth: 0, class: 0, mean prob. 0.0000, 94% HDI: [0.0000,0.0000]
ground-truth: 0, class: 0, mean prob. 0.0000, 94% HDI: [0.0000,0.0000]
ground-truth: 0, class: 0, mean prob. 0.0824, 94% HDI: [0.0418,0.1357]
ground-truth: 0, class: 0, mean prob. 0.4835, 94% HDI: [0.3946,0.5687]
ground-truth: 0, class: 0, mean prob. 0.3333, 94% HDI: [0.2363,0.4422]
ground-truth: 0, class: 0, mean prob. 0.0000, 94% HDI: [0.0000,0.0001]
ground-truth: 1, class: 1, mean prob. 0.7865, 94% HDI: [0.7080,0.8517]
ground-truth: 1, class: 1, mean prob. 0.9867, 94% HDI: [0.9769,0.9935]
ground-truth: 1, class: 1, mean prob. 0.9758, 94% HDI: [0.9585,0.9877]
ground-truth: 0, class: 0, mean prob. 0.0236, 94% HDI: [0.0094,0.0467]
ground-truth: 1, class: 1, mean prob. 0.9850, 94% HDI: [0.9740,0.9925]
ground-truth: 0, class: 0, mean prob. 0.0000, 94% HDI: [0.0000,0.0000]
ground-truth: 0, class: 0, mean prob. 0.0000, 94% HDI: [0.0000,0.0002]
ground-truth: 1, class: 1, mean prob. 0.8380, 94% HDI: [0.7810,0.8861]
ground-truth: 0, class: 0, mean prob. 0.0000, 94% HDI: [0.0000,0.0001]
ground-truth: 1, class: 1, mean prob. 0.9906, 94% HDI: [0.9830,0.9956]
ground-truth: 1, class: 1, mean prob. 0.9836, 94% HDI: [0.9712,0.9915]
ground-truth: 1, class: 1, mean prob. 0.9993, 94% HDI: [0.9982,0.9998]
ground-truth: 1, class: 1, mean prob. 0.9648, 94% HDI: [0.9436,0.9804]
ground-truth: 0, class: 0, mean prob. 0.0000, 94% HDI: [0.0000,0.0000]
ground-truth: 1, class: 1, mean prob. 0.9544, 94% HDI: [0.9072,0.9829]
ground-truth: 1, class: 1, mean prob. 0.9508, 94% HDI: [0.9127,0.9778]
ground-truth: 1, class: 1, mean prob. 0.9192, 94% HDI: [0.8261,0.9738]
ground-truth: 0, class: 0, mean prob. 0.3319, 94% HDI: [0.2357,0.4325]
ground-truth: 1, class: 1, mean prob. 0.9937, 94% HDI: [0.9879,0.9973]
ground-truth: 1, class: 1, mean prob. 0.9953, 94% HDI: [0.9904,0.9981]
ground-truth: 0, class: 1, mean prob. 0.6508, 94% HDI: [0.5463,0.7520]
ground-truth: 1, class: 1, mean prob. 0.9322, 94% HDI: [0.8904,0.9622]
ground-truth: 0, class: 0, mean prob. 0.4666, 94% HDI: [0.3525,0.5801]
ground-truth: 1, class: 1, mean prob. 0.9950, 94% HDI: [0.9887,0.9983]
ground-truth: 1, class: 1, mean prob. 0.9206, 94% HDI: [0.8853,0.9490]
ground-truth: 0, class: 0, mean prob. 0.0000, 94% HDI: [0.0000,0.0000]
ground-truth: 0, class: 0, mean prob. 0.0022, 94% HDI: [0.0006,0.0059]
ground-truth: 0, class: 0, mean prob. 0.0253, 94% HDI: [0.0063,0.0618]
ground-truth: 1, class: 1, mean prob. 0.9229, 94% HDI: [0.8825,0.9532]
ground-truth: 0, class: 0, mean prob. 0.0627, 94% HDI: [0.0291,0.1111]
ground-truth: 0, class: 0, mean prob. 0.0000, 94% HDI: [0.0000,0.0002]
ground-truth: 1, class: 1, mean prob. 0.9992, 94% HDI: [0.9981,0.9998]
ground-truth: 1, class: 1, mean prob. 0.9966, 94% HDI: [0.9923,0.9988]
ground-truth: 1, class: 1, mean prob. 0.9916, 94% HDI: [0.9836,0.9965]
ground-truth: 0, class: 0, mean prob. 0.0195, 94% HDI: [0.0066,0.0430]
ground-truth: 1, class: 1, mean prob. 0.9960, 94% HDI: [0.9923,0.9984]
ground-truth: 0, class: 0, mean prob. 0.1186, 94% HDI: [0.0697,0.1831]
ground-truth: 1, class: 1, mean prob. 0.9442, 94% HDI: [0.9115,0.9661]
ground-truth: 0, class: 1, mean prob. 0.6332, 94% HDI: [0.5319,0.7185]
ground-truth: 1, class: 1, mean prob. 0.9771, 94% HDI: [0.9640,0.9872]
ground-truth: 1, class: 1, mean prob. 0.9924, 94% HDI: [0.9860,0.9965]
ground-truth: 0, class: 0, mean prob. 0.0000, 94% HDI: [0.0000,0.0000]
ground-truth: 1, class: 1, mean prob. 0.9857, 94% HDI: [0.9737,0.9934]
ground-truth: 1, class: 1, mean prob. 0.9560, 94% HDI: [0.9296,0.9756]
ground-truth: 1, class: 1, mean prob. 0.9570, 94% HDI: [0.9348,0.9736]
ground-truth: 1, class: 1, mean prob. 0.9043, 94% HDI: [0.8429,0.9484]
ground-truth: 1, class: 1, mean prob. 0.9904, 94% HDI: [0.9807,0.9959]
ground-truth: 1, class: 1, mean prob. 0.9887, 94% HDI: [0.9785,0.9955]
ground-truth: 1, class: 1, mean prob. 0.9512, 94% HDI: [0.9207,0.9733]
ground-truth: 1, class: 1, mean prob. 0.9988, 94% HDI: [0.9968,0.9997]
ground-truth: 1, class: 1, mean prob. 0.9246, 94% HDI: [0.8848,0.9543]
ground-truth: 1, class: 1, mean prob. 0.8805, 94% HDI: [0.8267,0.9238]
ground-truth: 1, class: 1, mean prob. 0.9770, 94% HDI: [0.9593,0.9888]
ground-truth: 1, class: 1, mean prob. 0.9991, 94% HDI: [0.9974,0.9998]
ground-truth: 1, class: 1, mean prob. 0.9938, 94% HDI: [0.9880,0.9973]
ground-truth: 1, class: 1, mean prob. 0.9803, 94% HDI: [0.9654,0.9897]
ground-truth: 1, class: 1, mean prob. 0.9944, 94% HDI: [0.9862,0.9984]
ground-truth: 1, class: 1, mean prob. 0.9974, 94% HDI: [0.9941,0.9991]
ground-truth: 1, class: 1, mean prob. 0.9982, 94% HDI: [0.9957,0.9994]
ground-truth: 1, class: 1, mean prob. 0.9858, 94% HDI: [0.9752,0.9933]
ground-truth: 1, class: 1, mean prob. 0.9905, 94% HDI: [0.9831,0.9953]
ground-truth: 0, class: 0, mean prob. 0.0015, 94% HDI: [0.0003,0.0043]
ground-truth: 0, class: 0, mean prob. 0.0945, 94% HDI: [0.0389,0.1848]
ground-truth: 0, class: 0, mean prob. 0.0028, 94% HDI: [0.0005,0.0086]
ground-truth: 1, class: 1, mean prob. 0.9904, 94% HDI: [0.9822,0.9956]
ground-truth: 0, class: 0, mean prob. 0.0059, 94% HDI: [0.0017,0.0140]
ground-truth: 1, class: 1, mean prob. 0.9975, 94% HDI: [0.9946,0.9991]
ground-truth: 1, class: 1, mean prob. 0.9140, 94% HDI: [0.8804,0.9430]
ground-truth: 1, class: 0, mean prob. 0.4691, 94% HDI: [0.3239,0.6180]
ground-truth: 1, class: 1, mean prob. 0.9934, 94% HDI: [0.9868,0.9973]
ground-truth: 1, class: 1, mean prob. 0.9929, 94% HDI: [0.9868,0.9969]
ground-truth: 1, class: 1, mean prob. 0.9807, 94% HDI: [0.9661,0.9900]
ground-truth: 0, class: 0, mean prob. 0.0048, 94% HDI: [0.0011,0.0123]
ground-truth: 1, class: 1, mean prob. 0.9732, 94% HDI: [0.9515,0.9871]
ground-truth: 0, class: 0, mean prob. 0.2830, 94% HDI: [0.1459,0.4572]
ground-truth: 0, class: 0, mean prob. 0.0769, 94% HDI: [0.0316,0.1421]
ground-truth: 1, class: 1, mean prob. 0.9856, 94% HDI: [0.9751,0.9927]
ground-truth: 1, class: 1, mean prob. 0.7376, 94% HDI: [0.5955,0.8569]
ground-truth: 0, class: 0, mean prob. 0.0040, 94% HDI: [0.0010,0.0107]
ground-truth: 1, class: 1, mean prob. 0.9973, 94% HDI: [0.9941,0.9991]
ground-truth: 1, class: 1, mean prob. 0.9954, 94% HDI: [0.9905,0.9983]
ground-truth: 0, class: 1, mean prob. 0.5708, 94% HDI: [0.4547,0.6788]
ground-truth: 0, class: 0, mean prob. 0.0501, 94% HDI: [0.0252,0.0853]
ground-truth: 1, class: 1, mean prob. 0.9972, 94% HDI: [0.9939,0.9990]
ground-truth: 1, class: 1, mean prob. 0.9636, 94% HDI: [0.9354,0.9827]
ground-truth: 1, class: 1, mean prob. 0.9882, 94% HDI: [0.9787,0.9943]
ground-truth: 0, class: 0, mean prob. 0.0071, 94% HDI: [0.0023,0.0164]
ground-truth: 0, class: 0, mean prob. 0.0013, 94% HDI: [0.0002,0.0040]
ground-truth: 0, class: 0, mean prob. 0.0000, 94% HDI: [0.0000,0.0000]
ground-truth: 1, class: 1, mean prob. 0.9660, 94% HDI: [0.9475,0.9800]
ground-truth: 0, class: 0, mean prob. 0.0000, 94% HDI: [0.0000,0.0000]
=======================================

print(np.shape(yv_test), np.shape(class_assignments))
print(type(yv_test),type(class_assignments))

(143,) (143,)
<class 'numpy.ndarray'> <class 'numpy.ndarray'>

%pip install scikit-learn

Requirement already satisfied: scikit-learn in /usr/local/lib/python3.10/dist-packages (1.2.2)
Requirement already satisfied: numpy>=1.17.3 in /usr/local/lib/python3.10/dist-packages (from scikit-learn) (1.25.2)
Requirement already satisfied: scipy>=1.3.2 in /usr/local/lib/python3.10/dist-packages (from scikit-learn) (1.11.4)
Requirement already satisfied: joblib>=1.1.1 in /usr/local/lib/python3.10/dist-packages (from scikit-learn) (1.3.2)
Requirement already satisfied: threadpoolctl>=2.0.0 in /usr/local/lib/python3.10/dist-packages (from scikit-learn) (3.3.0)

from sklearn.metrics import accuracy_score, confusion_matrix

# Calculate Accuracy
accuracy = accuracy_score(yv_test, class_assignments)
print(f"Accuracy: {accuracy}")

# Calculate Confusion Matrix
conf_matrix = confusion_matrix(yv_test, class_assignments)
print(f"Confusion Matrix:\n{conf_matrix}")

Accuracy: 0.9370629370629371
Confusion Matrix:
[[46  8]
 [ 1 88]]

Analysis on Training Data#

logit_train = np.dot(xv_train, beta_chain.T) + alpha_chain
print(np.shape(logit))

probabilities_train = 1 / (1 + np.exp(-logit_train))
print(np.shape(probabilities_train))

(143, 1000)
(426, 1000)

# Average probabilities for prediction
mean_probabilities_train = np.mean(probabilities_train, axis=1)

# Class assignment (you might adjust the threshold if needed, default is 0.5)
class_assignments_train = (mean_probabilities_train > 0.5).astype(int)

# Uncertainty estimation
lower_bound_train = np.percentile(probabilities_train, 2.5, axis=1)
upper_bound_train = np.percentile(probabilities_train, 97.5, axis=1)

print("\n=======================================")
print("TRAINING DATA: \n", xv_train.T)
print("=======================================\n")

print("class, probabilities, ranges(94%HDI): ")
for g,h,i,j,k in zip(yv_train, class_assignments_train, mean_probabilities_train, lower_bound_train, upper_bound_train):
  print(f"ground-truth: {g}, class: {h}, mean prob. {i:.4f}, 94% HDI: [{j:.4f},{k:.4f}]")

print("=======================================\n")

=======================================
TRAINING DATA: 
 [[1.154e+01 2.031e+01 1.136e+01 ... 1.205e+01 2.044e+01 1.174e+01]
 [1.444e+01 2.706e+01 1.757e+01 ... 2.272e+01 2.178e+01 1.469e+01]
 [7.465e+01 1.329e+02 7.249e+01 ... 7.875e+01 1.338e+02 7.631e+01]
 ...
 [2.594e-02 9.333e-02 2.100e-02 ... 2.978e-02 7.785e-02 2.639e-02]
 [1.818e-01 1.814e-01 1.601e-01 ... 1.203e-01 1.618e-01 1.499e-01]
 [6.782e-02 5.572e-02 5.913e-02 ... 6.659e-02 5.557e-02 6.758e-02]]
=======================================

class, probabilities, ranges(94%HDI): 
ground-truth: 1, class: 1, mean prob. 0.9908, 94% HDI: [0.9824,0.9958]
ground-truth: 0, class: 0, mean prob. 0.0000, 94% HDI: [0.0000,0.0001]
ground-truth: 1, class: 1, mean prob. 0.9927, 94% HDI: [0.9865,0.9966]
ground-truth: 0, class: 0, mean prob. 0.1042, 94% HDI: [0.0483,0.1843]
ground-truth: 0, class: 0, mean prob. 0.0037, 94% HDI: [0.0008,0.0109]
ground-truth: 1, class: 1, mean prob. 0.7960, 94% HDI: [0.6794,0.8874]
ground-truth: 0, class: 0, mean prob. 0.0000, 94% HDI: [0.0000,0.0000]
ground-truth: 1, class: 1, mean prob. 0.9966, 94% HDI: [0.9925,0.9988]
ground-truth: 0, class: 1, mean prob. 0.5376, 94% HDI: [0.3663,0.6984]
ground-truth: 1, class: 1, mean prob. 0.9934, 94% HDI: [0.9872,0.9972]
ground-truth: 1, class: 1, mean prob. 0.9943, 94% HDI: [0.9867,0.9983]
ground-truth: 0, class: 0, mean prob. 0.3296, 94% HDI: [0.2068,0.4603]
ground-truth: 1, class: 1, mean prob. 0.9932, 94% HDI: [0.9839,0.9980]
ground-truth: 0, class: 0, mean prob. 0.0503, 94% HDI: [0.0176,0.1015]
ground-truth: 0, class: 0, mean prob. 0.0000, 94% HDI: [0.0000,0.0000]
ground-truth: 0, class: 0, mean prob. 0.2300, 94% HDI: [0.1556,0.3150]
ground-truth: 1, class: 1, mean prob. 0.8637, 94% HDI: [0.8154,0.9050]
ground-truth: 1, class: 1, mean prob. 0.9132, 94% HDI: [0.8660,0.9500]
ground-truth: 1, class: 1, mean prob. 0.9040, 94% HDI: [0.8497,0.9440]
ground-truth: 0, class: 0, mean prob. 0.1681, 94% HDI: [0.0792,0.3039]
ground-truth: 1, class: 0, mean prob. 0.2894, 94% HDI: [0.1584,0.4259]
ground-truth: 1, class: 1, mean prob. 0.9931, 94% HDI: [0.9864,0.9970]
ground-truth: 1, class: 1, mean prob. 0.9743, 94% HDI: [0.9516,0.9885]
ground-truth: 1, class: 1, mean prob. 0.9970, 94% HDI: [0.9892,0.9996]
ground-truth: 0, class: 0, mean prob. 0.0170, 94% HDI: [0.0064,0.0346]
ground-truth: 0, class: 0, mean prob. 0.0000, 94% HDI: [0.0000,0.0002]
ground-truth: 0, class: 0, mean prob. 0.0001, 94% HDI: [0.0000,0.0002]
ground-truth: 0, class: 1, mean prob. 0.8329, 94% HDI: [0.7451,0.9026]
ground-truth: 1, class: 1, mean prob. 0.8942, 94% HDI: [0.8290,0.9394]
ground-truth: 1, class: 1, mean prob. 0.9919, 94% HDI: [0.9834,0.9967]
ground-truth: 0, class: 0, mean prob. 0.0274, 94% HDI: [0.0093,0.0574]
ground-truth: 1, class: 1, mean prob. 0.9804, 94% HDI: [0.9668,0.9902]
ground-truth: 0, class: 0, mean prob. 0.0001, 94% HDI: [0.0000,0.0004]
ground-truth: 1, class: 1, mean prob. 0.8561, 94% HDI: [0.7595,0.9217]
ground-truth: 1, class: 1, mean prob. 0.8610, 94% HDI: [0.7909,0.9139]
ground-truth: 0, class: 0, mean prob. 0.0001, 94% HDI: [0.0000,0.0004]
ground-truth: 1, class: 1, mean prob. 0.9484, 94% HDI: [0.9117,0.9729]
ground-truth: 1, class: 1, mean prob. 0.9900, 94% HDI: [0.9784,0.9963]
ground-truth: 0, class: 0, mean prob. 0.0000, 94% HDI: [0.0000,0.0000]
ground-truth: 1, class: 1, mean prob. 0.9980, 94% HDI: [0.9954,0.9993]
ground-truth: 1, class: 1, mean prob. 0.9869, 94% HDI: [0.9772,0.9932]
ground-truth: 0, class: 0, mean prob. 0.0804, 94% HDI: [0.0377,0.1363]
ground-truth: 0, class: 0, mean prob. 0.0000, 94% HDI: [0.0000,0.0000]
ground-truth: 1, class: 1, mean prob. 0.9766, 94% HDI: [0.9614,0.9873]
ground-truth: 0, class: 0, mean prob. 0.0006, 94% HDI: [0.0001,0.0021]
ground-truth: 0, class: 1, mean prob. 0.5348, 94% HDI: [0.4366,0.6363]
ground-truth: 1, class: 1, mean prob. 0.9893, 94% HDI: [0.9807,0.9948]
ground-truth: 0, class: 0, mean prob. 0.0004, 94% HDI: [0.0000,0.0017]
ground-truth: 1, class: 1, mean prob. 0.9304, 94% HDI: [0.8978,0.9559]
ground-truth: 0, class: 0, mean prob. 0.0000, 94% HDI: [0.0000,0.0001]
ground-truth: 1, class: 1, mean prob. 0.9909, 94% HDI: [0.9830,0.9956]
ground-truth: 1, class: 1, mean prob. 0.8778, 94% HDI: [0.8179,0.9238]
ground-truth: 1, class: 1, mean prob. 0.9977, 94% HDI: [0.9948,0.9992]
ground-truth: 1, class: 1, mean prob. 0.9426, 94% HDI: [0.9163,0.9636]
ground-truth: 1, class: 1, mean prob. 0.9925, 94% HDI: [0.9850,0.9969]
ground-truth: 1, class: 1, mean prob. 0.5795, 94% HDI: [0.4750,0.6770]
ground-truth: 0, class: 0, mean prob. 0.0001, 94% HDI: [0.0000,0.0004]
ground-truth: 0, class: 0, mean prob. 0.0013, 94% HDI: [0.0002,0.0041]
ground-truth: 1, class: 1, mean prob. 0.9837, 94% HDI: [0.9721,0.9915]
ground-truth: 1, class: 1, mean prob. 0.6086, 94% HDI: [0.4702,0.7396]
ground-truth: 0, class: 0, mean prob. 0.0092, 94% HDI: [0.0027,0.0235]
ground-truth: 1, class: 0, mean prob. 0.4178, 94% HDI: [0.1866,0.6596]
ground-truth: 1, class: 1, mean prob. 0.9920, 94% HDI: [0.9856,0.9963]
ground-truth: 1, class: 1, mean prob. 0.9780, 94% HDI: [0.9576,0.9908]
ground-truth: 1, class: 1, mean prob. 0.9378, 94% HDI: [0.8897,0.9682]
ground-truth: 0, class: 0, mean prob. 0.0014, 94% HDI: [0.0002,0.0052]
ground-truth: 0, class: 1, mean prob. 0.7745, 94% HDI: [0.6815,0.8527]
ground-truth: 1, class: 1, mean prob. 0.9925, 94% HDI: [0.9865,0.9965]
ground-truth: 0, class: 1, mean prob. 0.8075, 94% HDI: [0.6847,0.8977]
ground-truth: 1, class: 1, mean prob. 0.9429, 94% HDI: [0.9042,0.9688]
ground-truth: 1, class: 1, mean prob. 0.9985, 94% HDI: [0.9963,0.9996]
ground-truth: 1, class: 1, mean prob. 0.9875, 94% HDI: [0.9742,0.9952]
ground-truth: 1, class: 1, mean prob. 0.7618, 94% HDI: [0.6868,0.8226]
ground-truth: 0, class: 0, mean prob. 0.0077, 94% HDI: [0.0024,0.0178]
ground-truth: 1, class: 1, mean prob. 0.9840, 94% HDI: [0.9735,0.9915]
ground-truth: 1, class: 1, mean prob. 0.9658, 94% HDI: [0.9472,0.9794]
ground-truth: 1, class: 1, mean prob. 0.9963, 94% HDI: [0.9924,0.9985]
ground-truth: 0, class: 0, mean prob. 0.0019, 94% HDI: [0.0003,0.0064]
ground-truth: 1, class: 1, mean prob. 0.9715, 94% HDI: [0.9465,0.9867]
ground-truth: 1, class: 1, mean prob. 0.9798, 94% HDI: [0.9637,0.9904]
ground-truth: 0, class: 0, mean prob. 0.0072, 94% HDI: [0.0015,0.0188]
ground-truth: 1, class: 1, mean prob. 0.9936, 94% HDI: [0.9864,0.9977]
ground-truth: 0, class: 0, mean prob. 0.0001, 94% HDI: [0.0000,0.0004]
ground-truth: 1, class: 1, mean prob. 0.9416, 94% HDI: [0.9125,0.9645]
ground-truth: 1, class: 1, mean prob. 0.7024, 94% HDI: [0.5463,0.8351]
ground-truth: 1, class: 1, mean prob. 0.9816, 94% HDI: [0.9671,0.9914]
ground-truth: 0, class: 0, mean prob. 0.2069, 94% HDI: [0.1354,0.2914]
ground-truth: 1, class: 1, mean prob. 0.9982, 94% HDI: [0.9957,0.9994]
ground-truth: 0, class: 0, mean prob. 0.1395, 94% HDI: [0.0545,0.2551]
ground-truth: 1, class: 1, mean prob. 0.9511, 94% HDI: [0.9152,0.9760]
ground-truth: 1, class: 1, mean prob. 0.9968, 94% HDI: [0.9933,0.9988]
ground-truth: 1, class: 1, mean prob. 0.8854, 94% HDI: [0.8365,0.9257]
ground-truth: 1, class: 1, mean prob. 0.9956, 94% HDI: [0.9914,0.9982]
ground-truth: 1, class: 1, mean prob. 0.9925, 94% HDI: [0.9857,0.9968]
ground-truth: 1, class: 1, mean prob. 0.9595, 94% HDI: [0.9311,0.9793]
ground-truth: 1, class: 1, mean prob. 0.6976, 94% HDI: [0.5536,0.8192]
ground-truth: 0, class: 0, mean prob. 0.0864, 94% HDI: [0.0417,0.1457]
ground-truth: 0, class: 0, mean prob. 0.0001, 94% HDI: [0.0000,0.0004]
ground-truth: 1, class: 1, mean prob. 0.9244, 94% HDI: [0.8824,0.9574]
ground-truth: 1, class: 1, mean prob. 0.9970, 94% HDI: [0.9932,0.9990]
ground-truth: 1, class: 1, mean prob. 0.9822, 94% HDI: [0.9674,0.9917]
ground-truth: 1, class: 1, mean prob. 0.9535, 94% HDI: [0.9292,0.9733]
ground-truth: 1, class: 1, mean prob. 0.8492, 94% HDI: [0.7573,0.9210]
ground-truth: 0, class: 0, mean prob. 0.0041, 94% HDI: [0.0010,0.0107]
ground-truth: 1, class: 0, mean prob. 0.1323, 94% HDI: [0.0603,0.2306]
ground-truth: 1, class: 1, mean prob. 0.7236, 94% HDI: [0.5854,0.8412]
ground-truth: 1, class: 1, mean prob. 0.9620, 94% HDI: [0.9399,0.9783]
ground-truth: 0, class: 0, mean prob. 0.0000, 94% HDI: [0.0000,0.0000]
ground-truth: 1, class: 1, mean prob. 0.9970, 94% HDI: [0.9936,0.9989]
ground-truth: 1, class: 1, mean prob. 0.9869, 94% HDI: [0.9755,0.9940]
ground-truth: 1, class: 1, mean prob. 0.9907, 94% HDI: [0.9825,0.9958]
ground-truth: 1, class: 1, mean prob. 0.9790, 94% HDI: [0.9645,0.9887]
ground-truth: 0, class: 0, mean prob. 0.0000, 94% HDI: [0.0000,0.0000]
ground-truth: 0, class: 0, mean prob. 0.0052, 94% HDI: [0.0012,0.0151]
ground-truth: 1, class: 1, mean prob. 0.9834, 94% HDI: [0.9657,0.9935]
ground-truth: 0, class: 1, mean prob. 0.7498, 94% HDI: [0.6484,0.8354]
ground-truth: 0, class: 0, mean prob. 0.0154, 94% HDI: [0.0028,0.0440]
ground-truth: 1, class: 1, mean prob. 0.8026, 94% HDI: [0.6419,0.9156]
ground-truth: 1, class: 1, mean prob. 0.9315, 94% HDI: [0.8984,0.9580]
ground-truth: 1, class: 1, mean prob. 0.8399, 94% HDI: [0.7790,0.8946]
ground-truth: 1, class: 1, mean prob. 0.9873, 94% HDI: [0.9764,0.9943]
ground-truth: 0, class: 0, mean prob. 0.0617, 94% HDI: [0.0306,0.1059]
ground-truth: 1, class: 1, mean prob. 0.5250, 94% HDI: [0.3751,0.6701]
ground-truth: 1, class: 0, mean prob. 0.3167, 94% HDI: [0.1832,0.4636]
ground-truth: 1, class: 0, mean prob. 0.4832, 94% HDI: [0.3009,0.6731]
ground-truth: 1, class: 1, mean prob. 0.9100, 94% HDI: [0.8608,0.9471]
ground-truth: 1, class: 1, mean prob. 0.9555, 94% HDI: [0.9298,0.9755]
ground-truth: 1, class: 1, mean prob. 0.9842, 94% HDI: [0.9723,0.9922]
ground-truth: 0, class: 1, mean prob. 0.6390, 94% HDI: [0.5047,0.7623]
ground-truth: 1, class: 1, mean prob. 0.9842, 94% HDI: [0.9709,0.9928]
ground-truth: 1, class: 1, mean prob. 0.5798, 94% HDI: [0.4790,0.6856]
ground-truth: 0, class: 0, mean prob. 0.0000, 94% HDI: [0.0000,0.0000]
ground-truth: 1, class: 1, mean prob. 0.9968, 94% HDI: [0.9931,0.9988]
ground-truth: 1, class: 1, mean prob. 0.9981, 94% HDI: [0.9961,0.9993]
ground-truth: 1, class: 1, mean prob. 0.9930, 94% HDI: [0.9862,0.9970]
ground-truth: 1, class: 1, mean prob. 0.9987, 94% HDI: [0.9967,0.9996]
ground-truth: 1, class: 1, mean prob. 0.9246, 94% HDI: [0.8868,0.9558]
ground-truth: 0, class: 0, mean prob. 0.0010, 94% HDI: [0.0002,0.0030]
ground-truth: 1, class: 0, mean prob. 0.4639, 94% HDI: [0.2895,0.6467]
ground-truth: 1, class: 1, mean prob. 0.9262, 94% HDI: [0.8925,0.9529]
ground-truth: 1, class: 1, mean prob. 0.9483, 94% HDI: [0.9025,0.9762]
ground-truth: 0, class: 0, mean prob. 0.0000, 94% HDI: [0.0000,0.0000]
ground-truth: 1, class: 1, mean prob. 0.9678, 94% HDI: [0.9282,0.9894]
ground-truth: 1, class: 1, mean prob. 0.9652, 94% HDI: [0.9402,0.9812]
ground-truth: 0, class: 0, mean prob. 0.0699, 94% HDI: [0.0280,0.1414]
ground-truth: 1, class: 1, mean prob. 0.7172, 94% HDI: [0.5904,0.8292]
ground-truth: 1, class: 1, mean prob. 0.9748, 94% HDI: [0.9411,0.9917]
ground-truth: 0, class: 0, mean prob. 0.0000, 94% HDI: [0.0000,0.0001]
ground-truth: 1, class: 1, mean prob. 0.6932, 94% HDI: [0.6113,0.7666]
ground-truth: 0, class: 0, mean prob. 0.0018, 94% HDI: [0.0004,0.0050]
ground-truth: 1, class: 1, mean prob. 0.9848, 94% HDI: [0.9725,0.9929]
ground-truth: 1, class: 1, mean prob. 0.9978, 94% HDI: [0.9949,0.9992]
ground-truth: 1, class: 1, mean prob. 0.7199, 94% HDI: [0.5944,0.8274]
ground-truth: 1, class: 1, mean prob. 0.9778, 94% HDI: [0.9625,0.9885]
ground-truth: 1, class: 1, mean prob. 0.9702, 94% HDI: [0.9525,0.9835]
ground-truth: 1, class: 1, mean prob. 0.9699, 94% HDI: [0.9538,0.9824]
ground-truth: 0, class: 0, mean prob. 0.0014, 94% HDI: [0.0003,0.0037]
ground-truth: 0, class: 0, mean prob. 0.0044, 94% HDI: [0.0011,0.0114]
ground-truth: 0, class: 0, mean prob. 0.0001, 94% HDI: [0.0000,0.0004]
ground-truth: 0, class: 0, mean prob. 0.0001, 94% HDI: [0.0000,0.0006]
ground-truth: 0, class: 0, mean prob. 0.0005, 94% HDI: [0.0001,0.0018]
ground-truth: 1, class: 1, mean prob. 0.9324, 94% HDI: [0.8993,0.9588]
ground-truth: 1, class: 1, mean prob. 0.9895, 94% HDI: [0.9803,0.9952]
ground-truth: 0, class: 0, mean prob. 0.0037, 94% HDI: [0.0005,0.0125]
ground-truth: 1, class: 1, mean prob. 0.9713, 94% HDI: [0.9531,0.9848]
ground-truth: 0, class: 1, mean prob. 0.7385, 94% HDI: [0.6548,0.8179]
ground-truth: 1, class: 1, mean prob. 0.6536, 94% HDI: [0.3068,0.9065]
ground-truth: 1, class: 1, mean prob. 0.9977, 94% HDI: [0.9952,0.9991]
ground-truth: 1, class: 1, mean prob. 0.9754, 94% HDI: [0.9566,0.9874]
ground-truth: 1, class: 1, mean prob. 0.9610, 94% HDI: [0.9403,0.9773]
ground-truth: 0, class: 0, mean prob. 0.2150, 94% HDI: [0.1311,0.3164]
ground-truth: 0, class: 0, mean prob. 0.0000, 94% HDI: [0.0000,0.0002]
ground-truth: 0, class: 0, mean prob. 0.0066, 94% HDI: [0.0017,0.0166]
ground-truth: 0, class: 0, mean prob. 0.0124, 94% HDI: [0.0035,0.0297]
ground-truth: 1, class: 1, mean prob. 0.9854, 94% HDI: [0.9748,0.9926]
ground-truth: 1, class: 1, mean prob. 0.9825, 94% HDI: [0.9608,0.9942]
ground-truth: 0, class: 0, mean prob. 0.0000, 94% HDI: [0.0000,0.0000]
ground-truth: 0, class: 0, mean prob. 0.0177, 94% HDI: [0.0057,0.0400]
ground-truth: 0, class: 1, mean prob. 0.8187, 94% HDI: [0.7580,0.8689]
ground-truth: 1, class: 1, mean prob. 0.9928, 94% HDI: [0.9862,0.9969]
ground-truth: 1, class: 1, mean prob. 0.7348, 94% HDI: [0.6301,0.8270]
ground-truth: 1, class: 1, mean prob. 0.8151, 94% HDI: [0.6457,0.9307]
ground-truth: 1, class: 1, mean prob. 0.9555, 94% HDI: [0.9304,0.9733]
ground-truth: 0, class: 0, mean prob. 0.0006, 94% HDI: [0.0001,0.0020]
ground-truth: 0, class: 0, mean prob. 0.0004, 94% HDI: [0.0001,0.0015]
ground-truth: 1, class: 1, mean prob. 0.9298, 94% HDI: [0.8882,0.9588]
ground-truth: 1, class: 1, mean prob. 0.9894, 94% HDI: [0.9784,0.9956]
ground-truth: 0, class: 0, mean prob. 0.0873, 94% HDI: [0.0404,0.1546]
ground-truth: 1, class: 1, mean prob. 0.9388, 94% HDI: [0.8953,0.9692]
ground-truth: 0, class: 0, mean prob. 0.4636, 94% HDI: [0.3445,0.5785]
ground-truth: 0, class: 0, mean prob. 0.0135, 94% HDI: [0.0038,0.0325]
ground-truth: 1, class: 1, mean prob. 0.9653, 94% HDI: [0.9460,0.9795]
ground-truth: 1, class: 1, mean prob. 0.9657, 94% HDI: [0.9458,0.9802]
ground-truth: 1, class: 1, mean prob. 0.9672, 94% HDI: [0.9465,0.9823]
ground-truth: 1, class: 1, mean prob. 0.9861, 94% HDI: [0.9742,0.9935]
ground-truth: 1, class: 1, mean prob. 0.9934, 94% HDI: [0.9872,0.9970]
ground-truth: 1, class: 1, mean prob. 0.9928, 94% HDI: [0.9862,0.9967]
ground-truth: 1, class: 1, mean prob. 0.8636, 94% HDI: [0.7777,0.9286]
ground-truth: 1, class: 0, mean prob. 0.4235, 94% HDI: [0.2935,0.5578]
ground-truth: 0, class: 1, mean prob. 0.7137, 94% HDI: [0.6349,0.7876]
ground-truth: 1, class: 1, mean prob. 0.9980, 94% HDI: [0.9949,0.9995]
ground-truth: 1, class: 1, mean prob. 0.9939, 94% HDI: [0.9877,0.9977]
ground-truth: 0, class: 0, mean prob. 0.0048, 94% HDI: [0.0014,0.0114]
ground-truth: 0, class: 0, mean prob. 0.0139, 94% HDI: [0.0043,0.0322]
ground-truth: 1, class: 1, mean prob. 0.9910, 94% HDI: [0.9832,0.9959]
ground-truth: 1, class: 1, mean prob. 0.9793, 94% HDI: [0.9648,0.9895]
ground-truth: 1, class: 1, mean prob. 0.9942, 94% HDI: [0.9884,0.9975]
ground-truth: 0, class: 0, mean prob. 0.0000, 94% HDI: [0.0000,0.0001]
ground-truth: 1, class: 1, mean prob. 0.9666, 94% HDI: [0.9413,0.9830]
ground-truth: 0, class: 0, mean prob. 0.1121, 94% HDI: [0.0576,0.1857]
ground-truth: 1, class: 1, mean prob. 0.7634, 94% HDI: [0.6858,0.8317]
ground-truth: 1, class: 1, mean prob. 0.8903, 94% HDI: [0.8394,0.9306]
ground-truth: 0, class: 0, mean prob. 0.4042, 94% HDI: [0.2759,0.5379]
ground-truth: 1, class: 1, mean prob. 0.5648, 94% HDI: [0.4453,0.6807]
ground-truth: 0, class: 0, mean prob. 0.0113, 94% HDI: [0.0035,0.0264]
ground-truth: 1, class: 1, mean prob. 0.9340, 94% HDI: [0.9049,0.9576]
ground-truth: 0, class: 0, mean prob. 0.1082, 94% HDI: [0.0465,0.1948]
ground-truth: 1, class: 1, mean prob. 0.9728, 94% HDI: [0.9547,0.9857]
ground-truth: 1, class: 1, mean prob. 0.9900, 94% HDI: [0.9811,0.9956]
ground-truth: 0, class: 0, mean prob. 0.0016, 94% HDI: [0.0002,0.0062]
ground-truth: 0, class: 0, mean prob. 0.0353, 94% HDI: [0.0106,0.0807]
ground-truth: 1, class: 1, mean prob. 0.9946, 94% HDI: [0.9895,0.9977]
ground-truth: 1, class: 1, mean prob. 0.9849, 94% HDI: [0.9730,0.9926]
ground-truth: 0, class: 0, mean prob. 0.0000, 94% HDI: [0.0000,0.0000]
ground-truth: 1, class: 0, mean prob. 0.0301, 94% HDI: [0.0063,0.0850]
ground-truth: 1, class: 1, mean prob. 0.9847, 94% HDI: [0.9734,0.9921]
ground-truth: 0, class: 1, mean prob. 0.5657, 94% HDI: [0.4568,0.6698]
ground-truth: 0, class: 0, mean prob. 0.0001, 94% HDI: [0.0000,0.0004]
ground-truth: 1, class: 1, mean prob. 0.9889, 94% HDI: [0.9694,0.9976]
ground-truth: 1, class: 1, mean prob. 0.9894, 94% HDI: [0.9791,0.9958]
ground-truth: 1, class: 1, mean prob. 0.9855, 94% HDI: [0.9744,0.9929]
ground-truth: 1, class: 1, mean prob. 0.9173, 94% HDI: [0.8813,0.9490]
ground-truth: 1, class: 1, mean prob. 0.7938, 94% HDI: [0.6821,0.8791]
ground-truth: 1, class: 1, mean prob. 0.9942, 94% HDI: [0.9886,0.9977]
ground-truth: 0, class: 0, mean prob. 0.0239, 94% HDI: [0.0084,0.0496]
ground-truth: 1, class: 1, mean prob. 0.9968, 94% HDI: [0.9927,0.9990]
ground-truth: 1, class: 1, mean prob. 0.9923, 94% HDI: [0.9856,0.9965]
ground-truth: 0, class: 0, mean prob. 0.0000, 94% HDI: [0.0000,0.0000]
ground-truth: 0, class: 0, mean prob. 0.0001, 94% HDI: [0.0000,0.0005]
ground-truth: 1, class: 1, mean prob. 0.9905, 94% HDI: [0.9817,0.9959]
ground-truth: 1, class: 1, mean prob. 0.9984, 94% HDI: [0.9961,0.9995]
ground-truth: 1, class: 1, mean prob. 0.9861, 94% HDI: [0.9757,0.9933]
ground-truth: 0, class: 0, mean prob. 0.0234, 94% HDI: [0.0072,0.0535]
ground-truth: 1, class: 1, mean prob. 0.9922, 94% HDI: [0.9852,0.9967]
ground-truth: 1, class: 1, mean prob. 0.9979, 94% HDI: [0.9953,0.9992]
ground-truth: 1, class: 1, mean prob. 0.9860, 94% HDI: [0.9739,0.9936]
ground-truth: 0, class: 0, mean prob. 0.0010, 94% HDI: [0.0002,0.0032]
ground-truth: 0, class: 0, mean prob. 0.0000, 94% HDI: [0.0000,0.0000]
ground-truth: 1, class: 1, mean prob. 0.9375, 94% HDI: [0.8843,0.9701]
ground-truth: 1, class: 1, mean prob. 0.9901, 94% HDI: [0.9803,0.9959]
ground-truth: 1, class: 1, mean prob. 0.9241, 94% HDI: [0.8752,0.9587]
ground-truth: 1, class: 1, mean prob. 0.9848, 94% HDI: [0.9737,0.9924]
ground-truth: 1, class: 1, mean prob. 0.9939, 94% HDI: [0.9881,0.9976]
ground-truth: 0, class: 0, mean prob. 0.0097, 94% HDI: [0.0023,0.0253]
ground-truth: 0, class: 1, mean prob. 0.8000, 94% HDI: [0.7174,0.8741]
ground-truth: 1, class: 0, mean prob. 0.2934, 94% HDI: [0.1648,0.4470]
ground-truth: 0, class: 0, mean prob. 0.3755, 94% HDI: [0.2663,0.4853]
ground-truth: 0, class: 0, mean prob. 0.0000, 94% HDI: [0.0000,0.0000]
ground-truth: 0, class: 0, mean prob. 0.0003, 94% HDI: [0.0000,0.0010]
ground-truth: 1, class: 1, mean prob. 0.9927, 94% HDI: [0.9823,0.9978]
ground-truth: 0, class: 0, mean prob. 0.0000, 94% HDI: [0.0000,0.0001]
ground-truth: 1, class: 1, mean prob. 0.9045, 94% HDI: [0.8533,0.9439]
ground-truth: 1, class: 1, mean prob. 0.9326, 94% HDI: [0.8871,0.9655]
ground-truth: 0, class: 0, mean prob. 0.0259, 94% HDI: [0.0091,0.0564]
ground-truth: 1, class: 1, mean prob. 0.9897, 94% HDI: [0.9812,0.9950]
ground-truth: 1, class: 1, mean prob. 0.9607, 94% HDI: [0.9378,0.9789]
ground-truth: 0, class: 1, mean prob. 0.7105, 94% HDI: [0.6303,0.7879]
ground-truth: 1, class: 1, mean prob. 0.9617, 94% HDI: [0.9180,0.9853]
ground-truth: 1, class: 1, mean prob. 0.9980, 94% HDI: [0.9954,0.9993]
ground-truth: 1, class: 1, mean prob. 0.9649, 94% HDI: [0.9249,0.9869]
ground-truth: 1, class: 0, mean prob. 0.3866, 94% HDI: [0.2471,0.5335]
ground-truth: 0, class: 1, mean prob. 0.9180, 94% HDI: [0.8823,0.9469]
ground-truth: 1, class: 1, mean prob. 0.8027, 94% HDI: [0.7333,0.8640]
ground-truth: 1, class: 1, mean prob. 0.9663, 94% HDI: [0.9433,0.9814]
ground-truth: 0, class: 0, mean prob. 0.1099, 94% HDI: [0.0588,0.1759]
ground-truth: 1, class: 1, mean prob. 0.9667, 94% HDI: [0.9431,0.9831]
ground-truth: 1, class: 1, mean prob. 0.9942, 94% HDI: [0.9879,0.9978]
ground-truth: 0, class: 0, mean prob. 0.1263, 94% HDI: [0.0564,0.2270]
ground-truth: 0, class: 0, mean prob. 0.0027, 94% HDI: [0.0006,0.0076]
ground-truth: 1, class: 1, mean prob. 0.9865, 94% HDI: [0.9756,0.9938]
ground-truth: 0, class: 0, mean prob. 0.0000, 94% HDI: [0.0000,0.0000]
ground-truth: 1, class: 1, mean prob. 0.9723, 94% HDI: [0.9513,0.9860]
ground-truth: 1, class: 1, mean prob. 0.9860, 94% HDI: [0.9685,0.9950]
ground-truth: 1, class: 1, mean prob. 0.9753, 94% HDI: [0.9584,0.9876]
ground-truth: 0, class: 0, mean prob. 0.1303, 94% HDI: [0.0387,0.2776]
ground-truth: 1, class: 1, mean prob. 0.9668, 94% HDI: [0.9413,0.9838]
ground-truth: 1, class: 1, mean prob. 0.9164, 94% HDI: [0.8522,0.9618]
ground-truth: 1, class: 1, mean prob. 0.9954, 94% HDI: [0.9906,0.9982]
ground-truth: 1, class: 1, mean prob. 0.9862, 94% HDI: [0.9757,0.9936]
ground-truth: 1, class: 1, mean prob. 0.9903, 94% HDI: [0.9806,0.9964]
ground-truth: 0, class: 0, mean prob. 0.2028, 94% HDI: [0.1241,0.2935]
ground-truth: 1, class: 1, mean prob. 0.9228, 94% HDI: [0.8878,0.9503]
ground-truth: 1, class: 1, mean prob. 0.9273, 94% HDI: [0.8227,0.9816]
ground-truth: 1, class: 1, mean prob. 0.9990, 94% HDI: [0.9974,0.9997]
ground-truth: 0, class: 0, mean prob. 0.0001, 94% HDI: [0.0000,0.0003]
ground-truth: 0, class: 0, mean prob. 0.0000, 94% HDI: [0.0000,0.0000]
ground-truth: 0, class: 0, mean prob. 0.0014, 94% HDI: [0.0002,0.0046]
ground-truth: 0, class: 0, mean prob. 0.0000, 94% HDI: [0.0000,0.0002]
ground-truth: 0, class: 0, mean prob. 0.0003, 94% HDI: [0.0000,0.0015]
ground-truth: 1, class: 1, mean prob. 0.9953, 94% HDI: [0.9886,0.9987]
ground-truth: 1, class: 1, mean prob. 0.9881, 94% HDI: [0.9744,0.9957]
ground-truth: 1, class: 1, mean prob. 0.9955, 94% HDI: [0.9889,0.9987]
ground-truth: 0, class: 0, mean prob. 0.2120, 94% HDI: [0.1029,0.3548]
ground-truth: 1, class: 1, mean prob. 0.9946, 94% HDI: [0.9895,0.9977]
ground-truth: 0, class: 1, mean prob. 0.5739, 94% HDI: [0.4602,0.6770]
ground-truth: 1, class: 0, mean prob. 0.4320, 94% HDI: [0.3335,0.5239]
ground-truth: 1, class: 1, mean prob. 0.9875, 94% HDI: [0.9775,0.9938]
ground-truth: 0, class: 0, mean prob. 0.0000, 94% HDI: [0.0000,0.0000]
ground-truth: 1, class: 1, mean prob. 0.9820, 94% HDI: [0.9696,0.9902]
ground-truth: 1, class: 1, mean prob. 0.9558, 94% HDI: [0.9341,0.9729]
ground-truth: 1, class: 1, mean prob. 0.8095, 94% HDI: [0.6862,0.9038]
ground-truth: 1, class: 1, mean prob. 0.9991, 94% HDI: [0.9978,0.9997]
ground-truth: 1, class: 1, mean prob. 0.9960, 94% HDI: [0.9921,0.9984]
ground-truth: 1, class: 1, mean prob. 0.9211, 94% HDI: [0.8839,0.9507]
ground-truth: 1, class: 1, mean prob. 0.9964, 94% HDI: [0.9906,0.9991]
ground-truth: 0, class: 0, mean prob. 0.4563, 94% HDI: [0.3617,0.5555]
ground-truth: 1, class: 1, mean prob. 0.9797, 94% HDI: [0.9657,0.9893]
ground-truth: 1, class: 1, mean prob. 0.9931, 94% HDI: [0.9870,0.9970]
ground-truth: 1, class: 1, mean prob. 0.7366, 94% HDI: [0.6200,0.8417]
ground-truth: 0, class: 1, mean prob. 0.6280, 94% HDI: [0.5361,0.7146]
ground-truth: 1, class: 1, mean prob. 0.9936, 94% HDI: [0.9877,0.9972]
ground-truth: 0, class: 0, mean prob. 0.3583, 94% HDI: [0.2235,0.5218]
ground-truth: 1, class: 1, mean prob. 0.9771, 94% HDI: [0.9359,0.9948]
ground-truth: 1, class: 1, mean prob. 0.9855, 94% HDI: [0.9670,0.9953]
ground-truth: 1, class: 1, mean prob. 0.9174, 94% HDI: [0.8776,0.9485]
ground-truth: 0, class: 0, mean prob. 0.2369, 94% HDI: [0.1443,0.3671]
ground-truth: 0, class: 0, mean prob. 0.0000, 94% HDI: [0.0000,0.0001]
ground-truth: 1, class: 1, mean prob. 0.8386, 94% HDI: [0.7660,0.8976]
ground-truth: 1, class: 1, mean prob. 0.9982, 94% HDI: [0.9957,0.9994]
ground-truth: 1, class: 1, mean prob. 0.9941, 94% HDI: [0.9880,0.9977]
ground-truth: 0, class: 0, mean prob. 0.0015, 94% HDI: [0.0002,0.0050]
ground-truth: 1, class: 1, mean prob. 0.9538, 94% HDI: [0.9300,0.9724]
ground-truth: 1, class: 1, mean prob. 0.9993, 94% HDI: [0.9982,0.9998]
ground-truth: 0, class: 0, mean prob. 0.0003, 94% HDI: [0.0000,0.0012]
ground-truth: 1, class: 1, mean prob. 0.8153, 94% HDI: [0.7060,0.8985]
ground-truth: 1, class: 1, mean prob. 0.9963, 94% HDI: [0.9923,0.9987]
ground-truth: 0, class: 0, mean prob. 0.0390, 94% HDI: [0.0110,0.0920]
ground-truth: 0, class: 0, mean prob. 0.0058, 94% HDI: [0.0010,0.0181]
ground-truth: 0, class: 0, mean prob. 0.0000, 94% HDI: [0.0000,0.0000]
ground-truth: 0, class: 0, mean prob. 0.0044, 94% HDI: [0.0010,0.0126]
ground-truth: 1, class: 1, mean prob. 0.9929, 94% HDI: [0.9861,0.9970]
ground-truth: 1, class: 1, mean prob. 0.7798, 94% HDI: [0.7076,0.8479]
ground-truth: 0, class: 0, mean prob. 0.0016, 94% HDI: [0.0003,0.0051]
ground-truth: 1, class: 1, mean prob. 0.9714, 94% HDI: [0.9516,0.9853]
ground-truth: 1, class: 1, mean prob. 0.7219, 94% HDI: [0.6453,0.7954]
ground-truth: 1, class: 1, mean prob. 0.9967, 94% HDI: [0.9933,0.9987]
ground-truth: 0, class: 0, mean prob. 0.4043, 94% HDI: [0.2531,0.5564]
ground-truth: 1, class: 1, mean prob. 0.9727, 94% HDI: [0.9507,0.9871]
ground-truth: 1, class: 1, mean prob. 0.9041, 94% HDI: [0.8216,0.9567]
ground-truth: 1, class: 1, mean prob. 0.9703, 94% HDI: [0.9536,0.9836]
ground-truth: 1, class: 1, mean prob. 0.9926, 94% HDI: [0.9849,0.9971]
ground-truth: 1, class: 1, mean prob. 0.9923, 94% HDI: [0.9853,0.9966]
ground-truth: 0, class: 0, mean prob. 0.1799, 94% HDI: [0.0683,0.3554]
ground-truth: 1, class: 1, mean prob. 0.9912, 94% HDI: [0.9836,0.9960]
ground-truth: 0, class: 0, mean prob. 0.0005, 94% HDI: [0.0001,0.0017]
ground-truth: 1, class: 1, mean prob. 0.9788, 94% HDI: [0.9645,0.9886]
ground-truth: 0, class: 0, mean prob. 0.0012, 94% HDI: [0.0002,0.0042]
ground-truth: 1, class: 1, mean prob. 0.9905, 94% HDI: [0.9831,0.9953]
ground-truth: 0, class: 0, mean prob. 0.0000, 94% HDI: [0.0000,0.0001]
ground-truth: 0, class: 0, mean prob. 0.0001, 94% HDI: [0.0000,0.0008]
ground-truth: 1, class: 1, mean prob. 0.9972, 94% HDI: [0.9942,0.9989]
ground-truth: 1, class: 1, mean prob. 0.9875, 94% HDI: [0.9770,0.9943]
ground-truth: 0, class: 0, mean prob. 0.0005, 94% HDI: [0.0000,0.0025]
ground-truth: 1, class: 1, mean prob. 0.7965, 94% HDI: [0.7145,0.8629]
ground-truth: 0, class: 0, mean prob. 0.0001, 94% HDI: [0.0000,0.0003]
ground-truth: 1, class: 1, mean prob. 0.9838, 94% HDI: [0.9708,0.9920]
ground-truth: 1, class: 1, mean prob. 0.9477, 94% HDI: [0.9124,0.9722]
ground-truth: 1, class: 1, mean prob. 0.9910, 94% HDI: [0.9828,0.9961]
ground-truth: 0, class: 0, mean prob. 0.0003, 94% HDI: [0.0000,0.0010]
ground-truth: 1, class: 1, mean prob. 0.9516, 94% HDI: [0.9178,0.9754]
ground-truth: 1, class: 1, mean prob. 0.9845, 94% HDI: [0.9720,0.9928]
ground-truth: 0, class: 0, mean prob. 0.0279, 94% HDI: [0.0073,0.0684]
ground-truth: 0, class: 0, mean prob. 0.0000, 94% HDI: [0.0000,0.0001]
ground-truth: 1, class: 1, mean prob. 0.9938, 94% HDI: [0.9871,0.9978]
ground-truth: 0, class: 0, mean prob. 0.0001, 94% HDI: [0.0000,0.0003]
ground-truth: 0, class: 1, mean prob. 0.7598, 94% HDI: [0.6824,0.8288]
ground-truth: 1, class: 1, mean prob. 0.9980, 94% HDI: [0.9954,0.9993]
ground-truth: 1, class: 1, mean prob. 0.9529, 94% HDI: [0.9238,0.9724]
ground-truth: 1, class: 1, mean prob. 0.9532, 94% HDI: [0.9159,0.9781]
ground-truth: 0, class: 0, mean prob. 0.0000, 94% HDI: [0.0000,0.0000]
ground-truth: 0, class: 0, mean prob. 0.2698, 94% HDI: [0.1771,0.3712]
ground-truth: 1, class: 1, mean prob. 0.9976, 94% HDI: [0.9946,0.9992]
ground-truth: 0, class: 0, mean prob. 0.0000, 94% HDI: [0.0000,0.0002]
ground-truth: 1, class: 1, mean prob. 0.9971, 94% HDI: [0.9935,0.9990]
ground-truth: 1, class: 1, mean prob. 0.7877, 94% HDI: [0.6582,0.8915]
ground-truth: 0, class: 1, mean prob. 0.6273, 94% HDI: [0.4399,0.7810]
ground-truth: 1, class: 1, mean prob. 0.9754, 94% HDI: [0.9597,0.9863]
ground-truth: 1, class: 1, mean prob. 0.9972, 94% HDI: [0.9937,0.9991]
ground-truth: 0, class: 0, mean prob. 0.0009, 94% HDI: [0.0001,0.0033]
ground-truth: 1, class: 0, mean prob. 0.2136, 94% HDI: [0.1145,0.3367]
ground-truth: 1, class: 1, mean prob. 0.9914, 94% HDI: [0.9840,0.9959]
ground-truth: 0, class: 0, mean prob. 0.0039, 94% HDI: [0.0008,0.0109]
ground-truth: 1, class: 1, mean prob. 0.9946, 94% HDI: [0.9877,0.9983]
ground-truth: 0, class: 0, mean prob. 0.0000, 94% HDI: [0.0000,0.0000]
ground-truth: 1, class: 1, mean prob. 0.9876, 94% HDI: [0.9753,0.9951]
ground-truth: 0, class: 1, mean prob. 0.5367, 94% HDI: [0.4448,0.6223]
ground-truth: 0, class: 1, mean prob. 0.9378, 94% HDI: [0.9065,0.9615]
ground-truth: 1, class: 1, mean prob. 0.9602, 94% HDI: [0.9296,0.9815]
ground-truth: 1, class: 1, mean prob. 0.9630, 94% HDI: [0.9091,0.9898]
ground-truth: 0, class: 0, mean prob. 0.0000, 94% HDI: [0.0000,0.0002]
ground-truth: 0, class: 1, mean prob. 0.6704, 94% HDI: [0.5819,0.7503]
ground-truth: 1, class: 1, mean prob. 0.7970, 94% HDI: [0.7239,0.8607]
ground-truth: 0, class: 0, mean prob. 0.0001, 94% HDI: [0.0000,0.0003]
ground-truth: 0, class: 0, mean prob. 0.0002, 94% HDI: [0.0000,0.0008]
ground-truth: 1, class: 1, mean prob. 0.8595, 94% HDI: [0.6728,0.9635]
ground-truth: 1, class: 0, mean prob. 0.4895, 94% HDI: [0.3299,0.6426]
ground-truth: 1, class: 1, mean prob. 0.9811, 94% HDI: [0.9681,0.9901]
ground-truth: 0, class: 0, mean prob. 0.0535, 94% HDI: [0.0217,0.1035]
ground-truth: 0, class: 0, mean prob. 0.0000, 94% HDI: [0.0000,0.0000]
ground-truth: 1, class: 1, mean prob. 0.9833, 94% HDI: [0.9710,0.9916]
ground-truth: 1, class: 1, mean prob. 0.8763, 94% HDI: [0.8223,0.9185]
ground-truth: 1, class: 1, mean prob. 0.9852, 94% HDI: [0.9737,0.9928]
ground-truth: 1, class: 1, mean prob. 0.8918, 94% HDI: [0.8488,0.9283]
ground-truth: 0, class: 1, mean prob. 0.8871, 94% HDI: [0.8285,0.9310]
ground-truth: 0, class: 1, mean prob. 0.7482, 94% HDI: [0.6645,0.8231]
ground-truth: 1, class: 1, mean prob. 0.9475, 94% HDI: [0.9130,0.9731]
ground-truth: 1, class: 1, mean prob. 0.9871, 94% HDI: [0.9762,0.9938]
ground-truth: 0, class: 0, mean prob. 0.3291, 94% HDI: [0.2270,0.4502]
ground-truth: 1, class: 1, mean prob. 0.9499, 94% HDI: [0.9031,0.9776]
ground-truth: 1, class: 1, mean prob. 0.9718, 94% HDI: [0.9547,0.9841]
ground-truth: 0, class: 0, mean prob. 0.0110, 94% HDI: [0.0035,0.0243]
ground-truth: 1, class: 1, mean prob. 0.9966, 94% HDI: [0.9927,0.9988]
ground-truth: 1, class: 1, mean prob. 0.9912, 94% HDI: [0.9822,0.9963]
ground-truth: 1, class: 1, mean prob. 0.8990, 94% HDI: [0.8318,0.9477]
ground-truth: 0, class: 0, mean prob. 0.0001, 94% HDI: [0.0000,0.0006]
ground-truth: 1, class: 1, mean prob. 0.9886, 94% HDI: [0.9786,0.9947]
=======================================

# Calculate Accuracy
accuracy_train = accuracy_score(yv_train, class_assignments_train)
print(f"Accuracy: {accuracy_train}")

# Calculate Confusion Matrix
conf_matrix_train = confusion_matrix(yv_train, class_assignments_train)
print(f"Confusion Matrix:\n{conf_matrix_train}")

Accuracy: 0.9154929577464789
Confusion Matrix:
[[135  23]
 [ 13 255]]

Isolate the misidentified events#

# Find indices where the prediction and the ground truth don't match
mismatch_indices = np.where(yv_test != class_assignments)[0]

# Select the mismatched events
mismatched_events_true = yv_test[mismatch_indices]
mismatched_events_class = class_assignments[mismatch_indices]
mismatched_events_prob = mean_probabilities[mismatch_indices]
mismatched_events_low = lower_bound[mismatch_indices]
mismatched_events_up = upper_bound[mismatch_indices]

print("\n=======================================")
print("MISMATCHED TEST DATA: \n", xv_train.T)
print("=======================================\n")

print("class, probabilities, ranges(94%HDI): ")
for f,g,h,i,j,k in zip(mismatch_indices, mismatched_events_true, mismatched_events_class, mismatched_events_prob, \
                     mismatched_events_low, mismatched_events_up ):
  print(f"index: {f:4}, ground-truth: {g}, class: {h}, mean prob. {i:.4f}, 94% HDI: [{j:.4f},{k:.4f}]")

print("=======================================\n")

=======================================
MISMATCHED TEST DATA: 
 [[1.154e+01 2.031e+01 1.136e+01 ... 1.205e+01 2.044e+01 1.174e+01]
 [1.444e+01 2.706e+01 1.757e+01 ... 2.272e+01 2.178e+01 1.469e+01]
 [7.465e+01 1.329e+02 7.249e+01 ... 7.875e+01 1.338e+02 7.631e+01]
 ...
 [2.594e-02 9.333e-02 2.100e-02 ... 2.978e-02 7.785e-02 2.639e-02]
 [1.818e-01 1.814e-01 1.601e-01 ... 1.203e-01 1.618e-01 1.499e-01]
 [6.782e-02 5.572e-02 5.913e-02 ... 6.659e-02 5.557e-02 6.758e-02]]
=======================================

class, probabilities, ranges(94%HDI): 
index:    7, ground-truth: 0, class: 1, mean prob. 0.9876, 94% HDI: [0.9773,0.9938]
index:   21, ground-truth: 0, class: 1, mean prob. 0.9401, 94% HDI: [0.9092,0.9642]
index:   30, ground-truth: 0, class: 1, mean prob. 0.7574, 94% HDI: [0.6417,0.8530]
index:   40, ground-truth: 0, class: 1, mean prob. 0.5834, 94% HDI: [0.4833,0.6747]
index:   42, ground-truth: 0, class: 1, mean prob. 0.5778, 94% HDI: [0.4193,0.7278]
index:   72, ground-truth: 0, class: 1, mean prob. 0.6508, 94% HDI: [0.5463,0.7520]
index:   90, ground-truth: 0, class: 1, mean prob. 0.6332, 94% HDI: [0.5319,0.7185]
index:  120, ground-truth: 1, class: 0, mean prob. 0.4691, 94% HDI: [0.3239,0.6180]
index:  133, ground-truth: 0, class: 1, mean prob. 0.5708, 94% HDI: [0.4547,0.6788]
=======================================

Filtering those events#

uncertain_events = [40,42,120,133]
uncertain_events = np.asarray(uncertain_events)

print(type(yv_test),np.shape(yv_test))

# Create a boolean mask
mask = np.ones(yv_test.shape, dtype=bool)  # Initialize mask with True
mask[uncertain_events] = False  # Set False for indices in mismatch_indices


# Filter the data
filtered_yv_test = yv_test[mask]
filtered_xv_test = xv_test[mask]
filtered_events_class = class_assignments[mask]
filtered_events_prob = mean_probabilities[mask]
filtered_events_low = lower_bound[mask]
filtered_events_up = upper_bound[mask]

<class 'numpy.ndarray'> (143,)

# Calculate Accuracy
accuracy_filter = accuracy_score(filtered_yv_test, filtered_events_class)
print(f"Accuracy: {accuracy_filter}")

# Calculate Confusion Matrix
conf_matrix_filter = confusion_matrix(filtered_yv_test, filtered_events_class)
print(f"Confusion Matrix:\n{conf_matrix_train}")

Accuracy: 0.9640287769784173
Confusion Matrix:
[[135  23]
 [ 13 255]]

Using PCA#

from sklearn.preprocessing import StandardScaler
from sklearn.decomposition import PCA

# Standardize the data
scaler = StandardScaler()
x_train_scaled = scaler.fit_transform(x_train)
x_test_scaled = scaler.transform(x_test)

# PCA transformation
pca = PCA(n_components=2)
x_train_pca = pca.fit_transform(x_train_scaled)
x_test_pca = pca.transform(x_test_scaled)

print(pca.explained_variance_)
expl_var = pca.explained_variance_ratio_
print(expl_var)
print(x_train_scaled.var())

[5.40185459 2.6218337 ]
[0.53891742 0.26156792]
0.9999999999999998

with pm.Model() as model_pca:

    alpha = pm.Normal('alpha', mu=0, sigma=5)
    betas = pm.Normal('betas', mu=0, sigma=5, shape= x_train_pca.shape[1])

    logits = alpha + pm.math.dot(x_train_pca, betas)

    theta = pm.Deterministic('theta', 1 / (1 + pm.math.exp(-logits)))
    bd = pm.Deterministic('bd', -alpha/betas[1] - betas[0]/betas[1] * x_train_pca[:,0])

    yl = pm.Bernoulli('yl', p=theta, observed=y_train)

    trace_pca = pm.sample(1000, tune=2000, return_inferencedata=True, target_accept=0.85)

100.00% [3000/3000 00:05<00:00 Sampling chain 0, 0 divergences]

100.00% [3000/3000 00:04<00:00 Sampling chain 1, 0 divergences]

az.summary(trace_pca)

	mean	sd	hdi_3%	hdi_97%	mcse_mean	mcse_sd	ess_bulk	ess_tail	r_hat
alpha	0.563	0.212	0.161	0.951	0.005	0.004	1610.0	1432.0	1.0
betas[0]	-2.489	0.297	-3.016	-1.901	0.008	0.006	1340.0	1294.0	1.0
betas[1]	0.789	0.164	0.465	1.065	0.004	0.003	1385.0	1183.0	1.0
theta[0]	0.989	0.006	0.977	0.998	0.000	0.000	1283.0	1044.0	1.0
theta[1]	0.000	0.000	0.000	0.001	0.000	0.000	1243.0	1188.0	1.0
...	...	...	...	...	...	...	...	...	...
bd[421]	-6.825	1.280	-9.212	-4.726	0.028	0.020	2044.0	1554.0	1.0
bd[422]	-4.389	0.860	-5.972	-2.989	0.019	0.014	1913.0	1609.0	1.0
bd[423]	-6.174	1.167	-8.342	-4.251	0.026	0.018	2027.0	1554.0	1.0
bd[424]	6.131	1.126	4.311	8.212	0.023	0.016	2331.0	1667.0	1.0
bd[425]	-6.511	1.225	-8.784	-4.513	0.027	0.019	2036.0	1554.0	1.0

855 rows × 9 columns

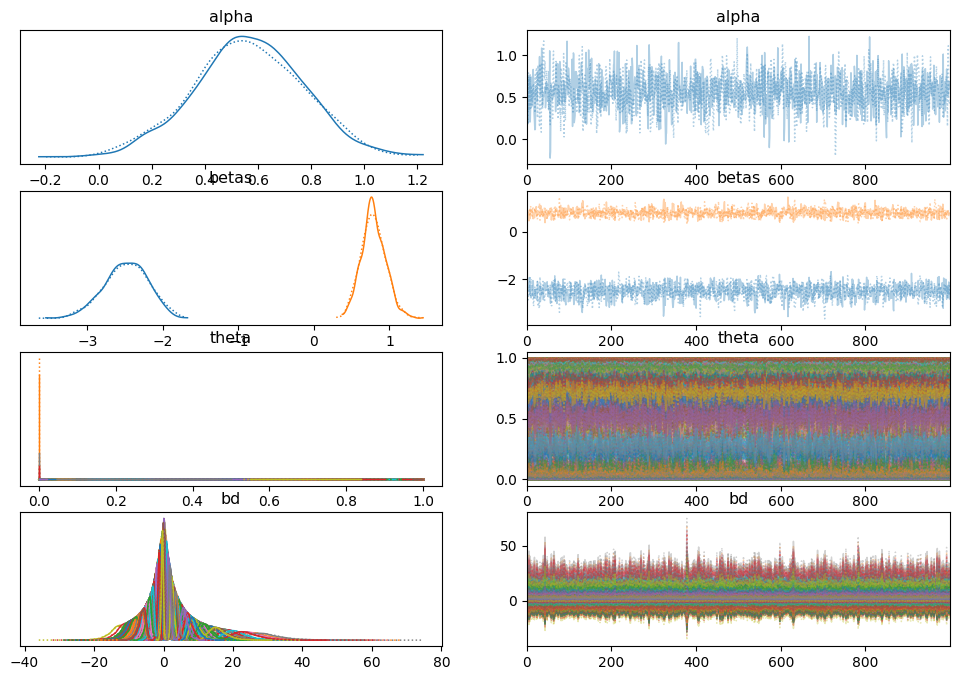
az.plot_trace(trace_pca)

array([[<Axes: title={'center': 'alpha'}>,
        <Axes: title={'center': 'alpha'}>],
       [<Axes: title={'center': 'betas'}>,
        <Axes: title={'center': 'betas'}>],
       [<Axes: title={'center': 'theta'}>,
        <Axes: title={'center': 'theta'}>],
       [<Axes: title={'center': 'bd'}>, <Axes: title={'center': 'bd'}>]],
      dtype=object)

alpha_chain_pca = trace_pca.posterior['alpha'].mean(axis=0).values
betas_chain_pca = trace_pca.posterior['betas'].mean(axis=0).values

print(np.shape(alpha_chain_pca), np.shape(betas_chain_pca))

(1000,) (1000, 2)

Analysis on standardized and PCA-reduced data#

logit_pca = np.dot(x_test_pca, betas_chain_pca.T) + alpha_chain_pca
print(np.shape(logit_pca))

probabilities_pca = 1 / (1 + np.exp(-logit_pca))
print(np.shape(probabilities_pca))

(143, 1000)
(143, 1000)

# Average probabilities for prediction
mean_probabilities_pca = np.mean(probabilities_pca, axis=1)

# Class assignment (you might adjust the threshold if needed, default is 0.5)
class_assignments_pca = (mean_probabilities_pca > 0.5).astype(int)

# Uncertainty estimation
lower_bound_pca = np.percentile(probabilities_pca, 2.5, axis=1)
upper_bound_pca = np.percentile(probabilities_pca, 97.5, axis=1)

print("\n=======================================")
print("TEST DATA (after stanardization and PCA-reduced): \n", x_test_pca.T)
print("=======================================\n")

print("class, probabilities, ranges(94%HDI): ")
count = 0
for g,h,i,j,k in zip(yv_test, class_assignments_pca, mean_probabilities_pca, lower_bound_pca, upper_bound_pca):
  if (count%20==0):
    print(f"ground-truth: {g}, class: {h}, mean prob. {i:.4f}, 94% HDI: [{j:.4f},{k:.4f}]")
  count = count+1

print("=======================================\n")

=======================================
TEST DATA (after stanardization and PCA-reduced): 
 [[-2.68765349 -2.5113037   1.01084219 -2.83111171  2.16544047  0.37694912
  -0.91817304 -1.68999278 -1.24530946  0.12623048 -2.38243235  1.90388123
   2.31888898 -2.27683002  2.83808936 -1.03028813 -2.29880578 -1.89687777
  -0.52039147 -1.30806695  4.36476664 -1.20633777 -1.33057932 -2.81543489
  -2.09760325  1.34545564  1.2317508  -1.91466512  0.44382841 -2.43543411
   1.28886213 -2.03699266 -1.28565306 -1.87007999  1.38979878 -2.2149903
  -0.99558582 -1.9069201  -2.10892453  2.78043943 -0.59618023 -1.71318561
   1.40232197 -0.59737643  0.8066522   0.17532421  4.02489799  7.51919622
   0.41079628  0.56903517  0.9351951   2.51774498 -0.71395051 -1.75754436
  -1.46500693  1.91261772 -1.52280955  3.52478866  4.13148745 -0.05593647
   4.92138927 -1.99454432 -1.10275494 -2.68566393 -0.73253818  7.77540963
  -2.67319268 -2.42506682 -1.12459722  0.43761454 -2.13246376 -2.04942915
  -0.39346898 -1.73509426 -0.01507782 -1.28842198 -0.5076413   4.31797969
   2.93628467  0.41471032 -0.28923594  1.67405133  2.92041367 -3.2609447
  -1.91768304 -2.04615302  2.0778711  -2.78127963  1.33931947 -1.54511781
   0.45081405 -1.38512919 -2.24308444  7.04517983 -1.4844696  -1.320075
  -1.06346831 -0.29988115 -1.10189236 -2.14063483 -1.74381292 -3.294123
  -1.21712346  0.22593737 -1.9337784  -3.02748172 -2.52695222 -1.26940837
  -2.41894358 -2.36448211 -3.45683486 -2.17811665 -2.07411438  2.60353705
   2.46462643  1.4679766  -1.74058593  2.79006312 -2.66861009 -0.69822168
  -0.2719495  -1.34396012 -2.3787894  -1.01556348  1.3896027  -0.33650935
   2.31255672  1.65456802 -1.69979833 -1.08656399  2.26569582 -2.72317747
  -2.85298563  0.47046889  1.90461237 -2.50982825 -1.34581768 -1.76283834
   2.86509754  2.78115429  4.38451616 -1.33134025  4.96953382]
 [-0.13611386  0.95862029 -1.91138315 -2.66288919 -0.72687977  0.38068157
   0.73713249  0.16453986 -1.80588348  2.40644672 -2.39874421 -0.51994523
   3.46739654 -0.83776882  1.3526116   0.26203505 -1.47888575 -0.55682945
   1.46265634  0.42854629 -1.98123104 -0.97801068 -0.87606965 -0.34930916
  -1.78494657 -0.90205228 -0.18292576 -0.07100387 -1.3986182   0.17726552
   3.22734351  1.34390113 -0.82187766  0.03418315  1.14438434 -0.77389129
  -0.99500946 -0.27751414 -0.99625037 -1.15343472 -1.41878682 -1.14861194
   0.84906373  0.72577427 -0.30001375  1.95294978 -0.92631825 -3.61025602
  -1.63897296  0.3996528   1.30361704 -3.11394172 -0.5566169  -0.53594595
  -0.81247219 -0.1500986   0.13347942 -3.31513936 -0.2582219   0.34122947
   1.7964115   0.03504414  1.1989128   0.39658141  1.0002434  -1.31888061
  -0.70000003 -1.2955354   3.41222897 -0.01454769  0.76648645  0.40705628
  -0.91087231 -1.49768481 -1.32694016  0.61004128  0.49457419 -1.70935433
   0.0558852  -2.50481596  1.08874529  0.51580252 -1.19841172 -0.90495962
  -0.25518624  1.03110911  1.65382569 -1.1361806  -0.01015888 -0.7460224
   1.18136689  0.02008071 -0.66894711 -0.91765443 -0.8289278   0.86895531
  -0.44478576  1.246291    1.4627026   1.36416819 -0.73090161  1.09375715
   0.20344261  1.23349178  0.14905164  1.77015587 -0.24862147  1.24576249
   2.50472344 -0.66023141 -0.29824417 -1.63495898 -0.42969605  0.12544955
   2.66458765 -1.82423955 -0.2261428   1.65936891 -0.9825544   0.41298155
  -0.64520053  1.03944042 -0.9356033   0.43087011 -0.9606564   0.94981272
   2.03762753  2.10182937 -0.23322591 -0.1132355   0.27211702 -1.75383072
   0.02007179  1.1177642   0.40762721  0.60242354 -1.53698874  0.13716864
   0.64051868 -0.93970368 -0.59959434  0.04264858 -2.13138555]]
=======================================

class, probabilities, ranges(94%HDI): 
ground-truth: 1, class: 1, mean prob. 0.9991, 94% HDI: [0.9977,0.9998]
ground-truth: 0, class: 0, mean prob. 0.0000, 94% HDI: [0.0000,0.0001]
ground-truth: 0, class: 1, mean prob. 0.7147, 94% HDI: [0.6275,0.7923]
ground-truth: 0, class: 0, mean prob. 0.0001, 94% HDI: [0.0000,0.0002]
ground-truth: 1, class: 1, mean prob. 0.8930, 94% HDI: [0.8476,0.9310]
ground-truth: 1, class: 1, mean prob. 0.9861, 94% HDI: [0.9753,0.9937]
ground-truth: 1, class: 1, mean prob. 0.6739, 94% HDI: [0.5983,0.7442]
ground-truth: 0, class: 0, mean prob. 0.0000, 94% HDI: [0.0000,0.0001]
=======================================

# Calculate Accuracy
accuracy_pca = accuracy_score(yv_test, class_assignments_pca)
print(f"Accuracy: {accuracy_pca}")

# Calculate Confusion Matrix
conf_matrix_pca = confusion_matrix(yv_test, class_assignments_pca)
print(f"Confusion Matrix:\n{conf_matrix_pca}")

Accuracy: 0.951048951048951
Confusion Matrix:
[[48  6]
 [ 1 88]]

Visualization of Uncertainty Band#

import matplotlib.pyplot as plt

idx = np.argsort(x_train_pca[:,0])

bd_mean = trace_pca.posterior['bd'].mean(axis=0).mean(axis=0)

plt.scatter(x_train_pca[:,0], x_train_pca[:,1], c=[f'C{x}' for x in yv_train])

bd = bd_mean[idx]

plt.plot(x_train_pca[:,0][idx], bd, color='k');

az.plot_hdi(x_train_pca[:,0], trace_pca.posterior['bd'], color='k')

plt.xlabel('PCA1')
plt.ylabel('PCA2')
plt.title('training data')

Text(0.5, 1.0, 'training data')

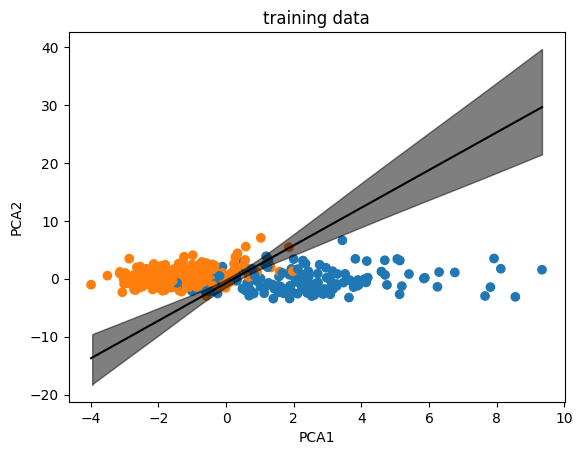
bd_mean = trace_pca.posterior['bd'].mean(axis=0).mean(axis=0)

plt.scatter(x_test_pca[:,0], x_test_pca[:,1], c=[f'C{x}' for x in yv_test])

bd = bd_mean[idx]

plt.plot(x_train_pca[:,0][idx], bd, color='k');

az.plot_hdi(x_train_pca[:,0], trace_pca.posterior['bd'], color='k')

plt.xlabel('PCA1')
plt.ylabel('PCA2')
plt.title('Test Data')

Text(0.5, 1.0, 'Test Data')

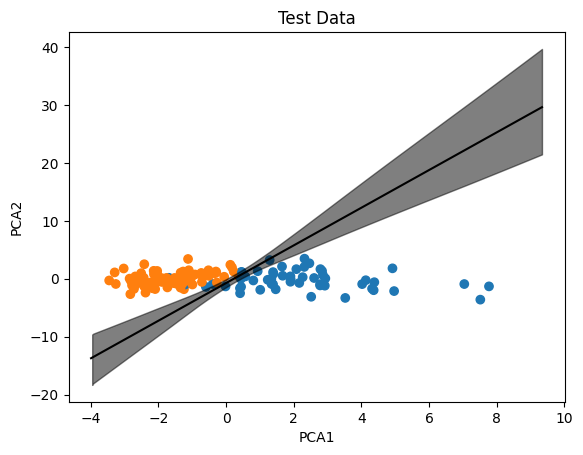
Filtering Events#

# Find indices where the prediction and the ground truth don't match
mismatch_indices = np.where(yv_test != class_assignments_pca)[0]
print(mismatch_indices)

[  5   7  21  40  72  90 133]

# Select the mismatched events
mismatched_events_true_pca = yv_test[mismatch_indices]
mismatched_events_class_pca = class_assignments_pca[mismatch_indices]
mismatched_events_prob_pca = mean_probabilities_pca[mismatch_indices]
mismatched_events_low_pca = lower_bound_pca[mismatch_indices]
mismatched_events_up_pca = upper_bound_pca[mismatch_indices]

print("\n=======================================")
print("MISMATCHED TEST DATA (after PCA): \n", xv_train.T)
print("=======================================\n")

print("class, probabilities, ranges(94%HDI): ")
for f,g,h,i,j,k in zip(mismatch_indices, mismatched_events_true_pca, mismatched_events_class_pca, mismatched_events_prob_pca, \
                     mismatched_events_low_pca, mismatched_events_up_pca ):
  print(f"index: {f:4}, ground-truth: {g}, class: {h}, mean prob. {i:.4f}, 94% HDI: [{j:.4f},{k:.4f}]")

print("=======================================\n")

=======================================
MISMATCHED TEST DATA (after PCA): 
 [[1.154e+01 2.031e+01 1.136e+01 ... 1.205e+01 2.044e+01 1.174e+01]
 [1.444e+01 2.706e+01 1.757e+01 ... 2.272e+01 2.178e+01 1.469e+01]
 [7.465e+01 1.329e+02 7.249e+01 ... 7.875e+01 1.338e+02 7.631e+01]
 ...
 [2.594e-02 9.333e-02 2.100e-02 ... 2.978e-02 7.785e-02 2.639e-02]
 [1.818e-01 1.814e-01 1.601e-01 ... 1.203e-01 1.618e-01 1.499e-01]
 [6.782e-02 5.572e-02 5.913e-02 ... 6.659e-02 5.557e-02 6.758e-02]]
=======================================

class, probabilities, ranges(94%HDI): 
index:    5, ground-truth: 1, class: 0, mean prob. 0.4813, 94% HDI: [0.4014,0.5575]
index:    7, ground-truth: 0, class: 1, mean prob. 0.9920, 94% HDI: [0.9847,0.9968]
index:   21, ground-truth: 0, class: 1, mean prob. 0.9407, 94% HDI: [0.9093,0.9652]
index:   40, ground-truth: 0, class: 1, mean prob. 0.7147, 94% HDI: [0.6275,0.7923]
index:   72, ground-truth: 0, class: 1, mean prob. 0.6937, 94% HDI: [0.6163,0.7643]
index:   90, ground-truth: 0, class: 1, mean prob. 0.5914, 94% HDI: [0.5029,0.6751]
index:  133, ground-truth: 0, class: 1, mean prob. 0.5674, 94% HDI: [0.4797,0.6527]
=======================================

uncertain_events_pca = [5,133]
uncertain_events_pca = np.asarray(uncertain_events_pca)

print(type(yv_test),np.shape(yv_test))

# Create a boolean mask
mask_pca = np.ones(yv_test.shape, dtype=bool)  # Initialize mask with True
mask_pca[uncertain_events_pca] = False  # Set False for indices in mismatch_indices


# Filter the data
filtered_yv_test_pca = yv_test[mask_pca]
filtered_xv_test_pca = x_test_pca.values[mask_pca]
filtered_events_class_pca = class_assignments_pca[mask_pca]
filtered_events_prob_pca = mean_probabilities_pca[mask_pca]
filtered_events_low_pca = lower_bound_pca[mask_pca]
filtered_events_up_pca = upper_bound_pca[mask_pca]

<class 'numpy.ndarray'> (143,)

Ple# Calculate Accuracy
accuracy_pca_filter = accuracy_score(filtered_yv_test_pca, filtered_events_class_pca)
print(f"Accuracy: {accuracy_pca_filter}")

# Calculate Confusion Matrix
conf_matrix_pca_filter = confusion_matrix(filtered_yv_test_pca, filtered_events_class_pca)
print(f"Confusion Matrix:\n{conf_matrix_pca}")

Accuracy: 0.9645390070921985
Confusion Matrix:
[[48  6]
 [ 1 88]]

Bayesian Reasoning in Data Science (DATA 644)

Assignment 2

Contents