Credits: Raschka et al, Chap 11
11. Building a Multi-layer Artificial Neural Network from Scratch#
from IPython.display import Image
%matplotlib inline
import numpy as np
import matplotlib.pyplot as plt
from IPython.display import display
display(Image(url="https://raw.githubusercontent.com/cfteach/NNDL_DATA621/webpage-src/DATA621/DATA621/images/multi-layer-NN.png", width=600))

11.1. Classifying handwritten digits#
The MNIST dataset is publicly available at http://yann.lecun.com/exdb/mnist/ and consists of the following four parts:
Training set images: train-images-idx3-ubyte.gz (9.9 MB, 47 MB unzipped, 60,000 examples)
Training set labels: train-labels-idx1-ubyte.gz (29 KB, 60 KB unzipped, 60,000 labels)
Test set images: t10k-images-idx3-ubyte.gz (1.6 MB, 7.8 MB, 10,000 examples)
Test set labels: t10k-labels-idx1-ubyte.gz (5 KB, 10 KB unzipped, 10,000 labels)
from sklearn.datasets import fetch_openml
X, y = fetch_openml('mnist_784', version=1, return_X_y=True)
X = X.values
y = y.astype(int).values
print(X.shape)
print(y.shape)
/usr/local/lib/python3.10/dist-packages/sklearn/datasets/_openml.py:1022: FutureWarning: The default value of `parser` will change from `'liac-arff'` to `'auto'` in 1.4. You can set `parser='auto'` to silence this warning. Therefore, an `ImportError` will be raised from 1.4 if the dataset is dense and pandas is not installed. Note that the pandas parser may return different data types. See the Notes Section in fetch_openml's API doc for details.
warn(
(70000, 784)
(70000,)
Normalize to [-1, 1] range:
X = ((X / 255.) - .5) * 2
print(X.shape)
(70000, 784)
# to familiarize
print(np.shape(X[y == 7])) # all digits == 7
print(np.shape(X[y == 7][2])) # visualize second example among those with label 7
(7293, 784)
(784,)
Visualize the first digit of each class:
import matplotlib.pyplot as plt
fig, ax = plt.subplots(nrows=2, ncols=5, sharex=True, sharey=True)
ax = ax.flatten()
for i in range(10):
img = X[y == i][10].reshape(28, 28) #creates a boolean mask with all images coincident with one specific digit. Of which we take the first.
ax[i].imshow(img, cmap='Greys')
ax[0].set_xticks([])
ax[0].set_yticks([])
plt.tight_layout()
plt.show()

Visualize 25 different versions of “7”:
fig, ax = plt.subplots(nrows=5, ncols=5, sharex=True, sharey=True)
ax = ax.flatten()
for i in range(25):
img = X[y == 7][i].reshape(28, 28)
ax[i].imshow(img, cmap='Greys')
ax[0].set_xticks([])
ax[0].set_yticks([])
plt.tight_layout()
# plt.savefig('figures/11_5.png', dpi=300)
plt.show()

Split into training, validation, and test set:
from sklearn.model_selection import train_test_split
X_temp, X_test, y_temp, y_test = train_test_split(
X, y, test_size=10000, random_state=123, stratify=y)
X_train, X_valid, y_train, y_valid = train_test_split(
X_temp, y_temp, test_size=5000, random_state=123, stratify=y_temp)
# optional to free up some memory by deleting non-used arrays:
del X_temp, y_temp, X, y
11.2. Modeling a Multi-Layer Perceptron (MLP)#
##########################
### MODEL
##########################
def sigmoid(z):
return 1. / (1. + np.exp(-z))
def int_to_onehot(y, num_labels):
ary = np.zeros((y.shape[0], num_labels)) # [n_examples, n_classes]
for i, val in enumerate(y):
ary[i, val] = 1
return ary
class InitializeModel:
def __init__(self, random_seed=123):
print("Model initialization")
self.random_seed = random_seed
# Set up a common random number generator
self.rng = np.random.RandomState(random_seed)
# Common attribute for all models
self.operation = "Initialization"
class NeuralNetMLP(InitializeModel):
def __init__(self, num_features, num_hidden, num_classes, random_seed=123):
super().__init__(random_seed)
"""
self.num_classes = num_classes
# hidden
#rng = np.random.RandomState(random_seed)
self.weight_h = self.rng.normal(
loc=0.0, scale=0.1, size=(num_hidden, num_features))
self.bias_h = np.zeros(num_hidden)
# output
self.weight_out = self.rng.normal(
loc=0.0, scale=0.1, size=(num_classes, num_hidden))
self.bias_out = np.zeros(num_classes)
"""
self.num_classes = num_classes
self.num_features = num_features
self.num_hidden = num_hidden
self._initialize_weights()
def _initialize_weights(self):
"""Initialize weights and biases with random values."""
# Initialize hidden layer weights and biases
self.weight_h = self.rng.normal(
loc=0.0, scale=0.1, size=(self.num_hidden, self.num_features))
self.bias_h = np.zeros(self.num_hidden)
# Initialize output layer weights and biases
self.weight_out = self.rng.normal(
loc=0.0, scale=0.1, size=(self.num_classes, self.num_hidden))
self.bias_out = np.zeros(self.num_classes)
def reinitialize(self, random_seed=None):
"""Reinitialize the model weights and biases if you need to."""
if random_seed is not None:
self.rng = np.random.RandomState(random_seed)
self._initialize_weights()
def forward(self, x):
# Hidden layer
# input dim: [n_examples, n_features] dot [n_hidden, n_features].T
# output dim: [n_examples, n_hidden]
z_h = np.dot(x, self.weight_h.T) + self.bias_h
a_h = sigmoid(z_h)
# Output layer
# input dim: [n_examples, n_hidden] dot [n_classes, n_hidden].T
# output dim: [n_examples, n_classes]
z_out = np.dot(a_h, self.weight_out.T) + self.bias_out
a_out = sigmoid(z_out)
return a_h, a_out
def backward(self, x, a_h, a_out, y):
#########################
### Output layer weights
#########################
# onehot encoding
y_onehot = int_to_onehot(y, self.num_classes)
# For simplicity, the loss function is assumed to be the same we saw in Adaline, that is an MSE
# Loss = 1/n \sum_{i=1}^{n} 1/t \sum_{j=1}^{t} (y^{i}_{j}-outa^{i}_{j})^2
# Later on we will look at other loss functions such as multi-category cross-entropy loss
# Part 1: dLoss/dOutWeights
## = dLoss/dOutAct * dOutAct/dOutZ * dOutz/dOutWeight
## where DeltaOut = dLoss/dOutAct * dOutAct/dOutZ
## for convenient re-use
# input/output dim: [n_examples, n_classes]
d_loss__d_a_out = 2.*(a_out - y_onehot) / y.shape[0]
# input/output dim: [n_examples, n_classes]
d_a_out__d_z_out = a_out * (1. - a_out) # sigmoid derivative (<--- demonstrate)
# output dim: [n_examples, n_classes]
delta_out = d_loss__d_a_out * d_a_out__d_z_out # "delta (rule) placeholder"
# gradient for output weights
# [n_examples, n_hidden]
d_z_out__dw_out = a_h
# input dim: [n_classes, n_examples] dot [n_examples, n_hidden]
# output dim: [n_classes, n_hidden]
d_loss__dw_out = np.dot(delta_out.T, d_z_out__dw_out)
d_loss__db_out = np.sum(delta_out, axis=0) # [n_classes]
#################################
# Part 2: dLoss/dHiddenWeights
## = DeltaOut * dOutZ/dHiddenAct * dHiddenAct/dHiddenZ * dHiddenZ/dWeight
# [n_classes, n_hidden]
d_z_out__a_h = self.weight_out
# output dim: [n_examples, n_hidden]
d_loss__a_h = np.dot(delta_out, d_z_out__a_h)
# [n_examples, n_hidden]
d_a_h__d_z_h = a_h * (1. - a_h) # sigmoid derivative
# [n_examples, n_features]
d_z_h__d_w_h = x
# output dim: [n_hidden, n_features]
d_loss__d_w_h = np.dot((d_loss__a_h * d_a_h__d_z_h).T, d_z_h__d_w_h)
d_loss__d_b_h = np.sum((d_loss__a_h * d_a_h__d_z_h), axis=0)
return (d_loss__dw_out, d_loss__db_out,
d_loss__d_w_h, d_loss__d_b_h)
#********************************************************#
#****************** THE MODEL *********************#
#********************************************************#
model = NeuralNetMLP(num_features=28*28,
num_hidden=50,
num_classes=10)
#********************************************************#
#********************************************************#
#********************************************************#
Model initialization
11.3. Coding the neural network training loop#
Defining data loaders:
num_epochs = 50
minibatch_size = 100
def minibatch_generator(X, y, minibatch_size):
indices = np.arange(X.shape[0]) # this is the number of examples
np.random.shuffle(indices)
for start_idx in range(0, indices.shape[0] - minibatch_size
+ 1, minibatch_size):
batch_idx = indices[start_idx:start_idx + minibatch_size]
yield X[batch_idx], y[batch_idx] # does not execute the function immediately, returs a generator object
#------------ let's check dimensionality --------------#
# iterate over training epochs
for i in range(num_epochs):
# iterate over minibatches
minibatch_gen = minibatch_generator(
X_train, y_train, minibatch_size)
for X_train_mini, y_train_mini in minibatch_gen:
break
break
print(X_train_mini.shape)
print(y_train_mini.shape)
(100, 784)
(100,)
Defining a function to compute the loss and accuracy
def mse_loss(targets, probas, num_labels=10):
onehot_targets = int_to_onehot(targets, num_labels=num_labels)
return np.mean((onehot_targets - probas)**2)
def accuracy(targets, predicted_labels):
return np.mean(predicted_labels == targets)
_, probas = model.forward(X_valid)
mse = mse_loss(y_valid, probas)
predicted_labels = np.argmax(probas, axis=1) # to label take the argument corresponding to the maximum probability among the 10 predicted probabilities
acc = accuracy(y_valid, predicted_labels)
print(f'Initial validation MSE: {mse:.1f}')
print(f'Initial validation accuracy: {acc*100:.1f}%')
Initial validation MSE: 0.3
Initial validation accuracy: 9.4%
# Initial validation MSE: 0.3
# Initial validation accuracy: 9.4%
# do these results make sense?
# at any given epoch
def compute_mse_and_acc(nnet, X, y, num_labels=10, minibatch_size=100):
mse, correct_pred, num_examples = 0., 0, 0
minibatch_gen = minibatch_generator(X, y, minibatch_size)
# compute through mini-batches: more memory efficient
for i, (features, targets) in enumerate(minibatch_gen):
_, probas = nnet.forward(features)
predicted_labels = np.argmax(probas, axis=1)
onehot_targets = int_to_onehot(targets, num_labels=num_labels)
loss = np.mean((onehot_targets - probas)**2)
correct_pred += (predicted_labels == targets).sum()
num_examples += targets.shape[0]
mse += loss
mse = mse/(i+1)
acc = correct_pred/num_examples
return mse, acc
mse, acc = compute_mse_and_acc(model, X_valid, y_valid)
print(f'Initial valid MSE: {mse:.1f}')
print(f'Initial valid accuracy: {acc*100:.1f}%')
Initial valid MSE: 0.3
Initial valid accuracy: 9.4%
def train(model, X_train, y_train, X_valid, y_valid, num_epochs,
learning_rate=0.1):
epoch_loss = []
epoch_train_acc = []
epoch_valid_acc = []
for e in range(num_epochs):
# iterate over minibatches
minibatch_gen = minibatch_generator(
X_train, y_train, minibatch_size)
for X_train_mini, y_train_mini in minibatch_gen:
#### Compute outputs ####
a_h, a_out = model.forward(X_train_mini)
#### Compute gradients ####
d_loss__d_w_out, d_loss__d_b_out, d_loss__d_w_h, d_loss__d_b_h = \
model.backward(X_train_mini, a_h, a_out, y_train_mini)
#### Update weights ####
model.weight_h -= learning_rate * d_loss__d_w_h
model.bias_h -= learning_rate * d_loss__d_b_h
model.weight_out -= learning_rate * d_loss__d_w_out
model.bias_out -= learning_rate * d_loss__d_b_out
#### Epoch Logging ####
train_mse, train_acc = compute_mse_and_acc(model, X_train, y_train)
valid_mse, valid_acc = compute_mse_and_acc(model, X_valid, y_valid)
train_acc, valid_acc = train_acc*100, valid_acc*100
epoch_train_acc.append(train_acc)
epoch_valid_acc.append(valid_acc)
epoch_loss.append(train_mse)
print(f'Epoch: {e+1:03d}/{num_epochs:03d} '
f'| Train MSE: {train_mse:.4f} '
f'| Train Acc: {train_acc:.2f}% '
f'| Valid Acc: {valid_acc:.2f}%')
return epoch_loss, epoch_train_acc, epoch_valid_acc
np.random.seed(123) # for the training set shuffling
#model.reinitialize()
epoch_loss, epoch_train_acc, epoch_valid_acc = train(
model, X_train, y_train, X_valid, y_valid,
num_epochs=40, learning_rate=0.1)
Epoch: 001/040 | Train MSE: 0.0134 | Train Acc: 92.42% | Valid Acc: 91.98%
Epoch: 002/040 | Train MSE: 0.0131 | Train Acc: 92.49% | Valid Acc: 92.14%
Epoch: 003/040 | Train MSE: 0.0128 | Train Acc: 92.68% | Valid Acc: 92.38%
Epoch: 004/040 | Train MSE: 0.0125 | Train Acc: 92.92% | Valid Acc: 92.68%
Epoch: 005/040 | Train MSE: 0.0123 | Train Acc: 93.07% | Valid Acc: 92.82%
Epoch: 006/040 | Train MSE: 0.0121 | Train Acc: 93.10% | Valid Acc: 92.88%
Epoch: 007/040 | Train MSE: 0.0119 | Train Acc: 93.28% | Valid Acc: 93.00%
Epoch: 008/040 | Train MSE: 0.0116 | Train Acc: 93.41% | Valid Acc: 93.02%
Epoch: 009/040 | Train MSE: 0.0114 | Train Acc: 93.51% | Valid Acc: 93.30%
Epoch: 010/040 | Train MSE: 0.0112 | Train Acc: 93.56% | Valid Acc: 93.30%
Epoch: 011/040 | Train MSE: 0.0111 | Train Acc: 93.72% | Valid Acc: 93.36%
Epoch: 012/040 | Train MSE: 0.0109 | Train Acc: 93.73% | Valid Acc: 93.52%
Epoch: 013/040 | Train MSE: 0.0108 | Train Acc: 93.81% | Valid Acc: 93.48%
Epoch: 014/040 | Train MSE: 0.0106 | Train Acc: 93.96% | Valid Acc: 93.46%
Epoch: 015/040 | Train MSE: 0.0105 | Train Acc: 94.07% | Valid Acc: 93.70%
Epoch: 016/040 | Train MSE: 0.0104 | Train Acc: 94.11% | Valid Acc: 93.86%
Epoch: 017/040 | Train MSE: 0.0102 | Train Acc: 94.17% | Valid Acc: 93.84%
Epoch: 018/040 | Train MSE: 0.0101 | Train Acc: 94.25% | Valid Acc: 93.84%
Epoch: 019/040 | Train MSE: 0.0100 | Train Acc: 94.37% | Valid Acc: 93.92%
Epoch: 020/040 | Train MSE: 0.0099 | Train Acc: 94.42% | Valid Acc: 93.96%
Epoch: 021/040 | Train MSE: 0.0098 | Train Acc: 94.52% | Valid Acc: 93.96%
Epoch: 022/040 | Train MSE: 0.0096 | Train Acc: 94.58% | Valid Acc: 93.90%
Epoch: 023/040 | Train MSE: 0.0095 | Train Acc: 94.61% | Valid Acc: 93.98%
Epoch: 024/040 | Train MSE: 0.0095 | Train Acc: 94.73% | Valid Acc: 94.12%
Epoch: 025/040 | Train MSE: 0.0094 | Train Acc: 94.71% | Valid Acc: 94.28%
Epoch: 026/040 | Train MSE: 0.0093 | Train Acc: 94.84% | Valid Acc: 94.26%
Epoch: 027/040 | Train MSE: 0.0092 | Train Acc: 94.82% | Valid Acc: 94.26%
Epoch: 028/040 | Train MSE: 0.0091 | Train Acc: 94.93% | Valid Acc: 94.32%
Epoch: 029/040 | Train MSE: 0.0090 | Train Acc: 95.00% | Valid Acc: 94.42%
Epoch: 030/040 | Train MSE: 0.0089 | Train Acc: 95.02% | Valid Acc: 94.22%
Epoch: 031/040 | Train MSE: 0.0088 | Train Acc: 95.12% | Valid Acc: 94.68%
Epoch: 032/040 | Train MSE: 0.0088 | Train Acc: 95.15% | Valid Acc: 94.50%
Epoch: 033/040 | Train MSE: 0.0088 | Train Acc: 95.13% | Valid Acc: 94.64%
Epoch: 034/040 | Train MSE: 0.0086 | Train Acc: 95.26% | Valid Acc: 94.66%
Epoch: 035/040 | Train MSE: 0.0085 | Train Acc: 95.27% | Valid Acc: 94.70%
Epoch: 036/040 | Train MSE: 0.0084 | Train Acc: 95.36% | Valid Acc: 94.88%
Epoch: 037/040 | Train MSE: 0.0084 | Train Acc: 95.36% | Valid Acc: 94.76%
Epoch: 038/040 | Train MSE: 0.0083 | Train Acc: 95.44% | Valid Acc: 94.90%
Epoch: 039/040 | Train MSE: 0.0083 | Train Acc: 95.46% | Valid Acc: 94.96%
Epoch: 040/040 | Train MSE: 0.0082 | Train Acc: 95.47% | Valid Acc: 94.76%
11.4. Evaluating the neural network performance#
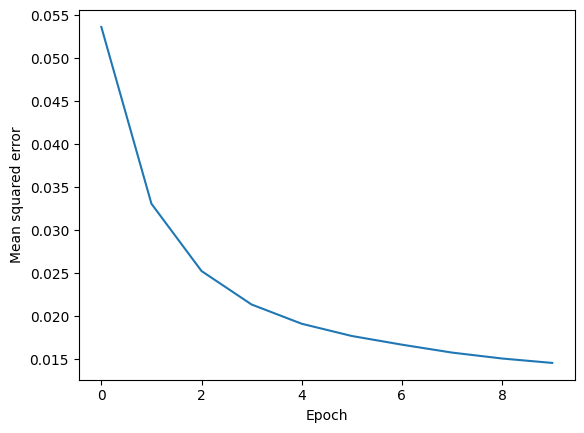
plt.plot(range(len(epoch_loss)), epoch_loss)
plt.ylabel('Mean squared error')
plt.xlabel('Epoch')
plt.show()
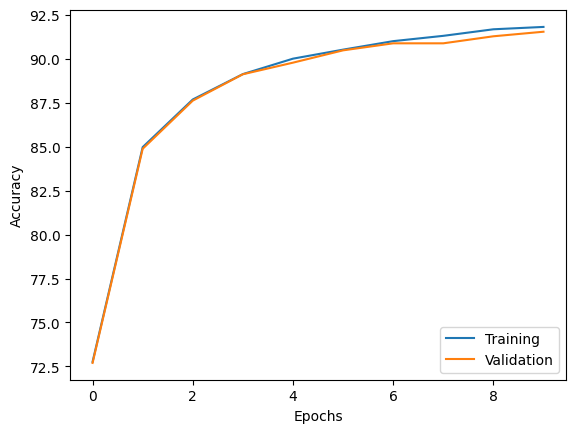
plt.plot(range(len(epoch_train_acc)), epoch_train_acc,
label='Training')
plt.plot(range(len(epoch_valid_acc)), epoch_valid_acc,
label='Validation')
plt.ylabel('Accuracy')
plt.xlabel('Epochs')
plt.legend(loc='lower right')
plt.show()
test_mse, test_acc = compute_mse_and_acc(model, X_test, y_test)
print(f'Test accuracy: {test_acc*100:.2f}%')
Test accuracy: 94.39%
11.5. Analysis of failed cases#
X_test_subset = X_test[:1000, :]
y_test_subset = y_test[:1000]
_, probas = model.forward(X_test_subset)
test_pred = np.argmax(probas, axis=1)
misclassified_images = X_test_subset[y_test_subset != test_pred][:25]
misclassified_labels = test_pred[y_test_subset != test_pred][:25]
correct_labels = y_test_subset[y_test_subset != test_pred][:25]
fig, ax = plt.subplots(nrows=5, ncols=5,
sharex=True, sharey=True, figsize=(8, 8))
ax = ax.flatten()
for i in range(25):
img = misclassified_images[i].reshape(28, 28)
ax[i].imshow(img, cmap='Greys', interpolation='nearest')
ax[i].set_title(f'{i+1}) '
f'True: {correct_labels[i]}\n'
f' Predicted: {misclassified_labels[i]}')
ax[0].set_xticks([])
ax[0].set_yticks([])
plt.tight_layout()
plt.show()

Some of these may not look challenging, still the network fails. For number 7, for example, we can guess that handwritten digit 7 with a horizontal line is underrepresented in our dataset and gets misclassified.
11.6. Other checks and further analysis#
Check image-level predictions
def plot_rand_digit(X,y):
tmp_indx = np.random.randint(len(X))
image_data = np.reshape(X[tmp_indx],(28, 28))
plt.imshow(image_data, cmap='gray')
plt.colorbar()
plt.show()
print("label is: ",y[tmp_indx])
return image_data,X[tmp_indx]
def plot_digit(tmp_indx, X,y):
image_data = np.reshape(X[tmp_indx],(28, 28))
plt.imshow(image_data, cmap='gray')
plt.colorbar()
plt.show()
print("label is: ",y[tmp_indx])
return image_data,X[tmp_indx]
def plot_image(image_data):
plt.imshow(image_data, cmap='gray')
plt.colorbar()
plt.show()
def image_2_X(tmp_image):
return tmp_image.reshape(28*28,)
tmp_image, tmp_imX = plot_rand_digit(X,y)
label is: 6
# Rotate the array by 90 degrees
rotated_image = np.rot90(tmp_image)
rotated_image = np.rot90(rotated_image)
plot_image(rotated_image)
tmp_X = image_2_X(rotated_image)
_, probas = model.forward(tmp_X)
rotated_pred = np.argmax(probas)
print("Predicted label is: ", rotated_pred)
Predicted label is: 7
Visualize in 3D-PCA
import pandas as pd
from sklearn.decomposition import PCA
import plotly.express as px
import plotly.io as pio
from google.colab import files
# Save the plot as an HTML file
def plot_3d_pca(X, y, target_names=None):
# Apply PCA with 3 components
pca = PCA(n_components=3)
X_pca = pca.fit_transform(X)
# Combine the PCA results and target labels
data = np.column_stack((X_pca, y))
# Create a DataFrame with column names
columns = ['PC1', 'PC2', 'PC3', 'label']
df = pd.DataFrame(data, columns=columns)
df['label'] = df['label'].astype(int)
if target_names is not None:
df['label_name'] = df['label'].apply(lambda x: target_names[x])
color_col = 'label_name'
else:
color_col = 'label'
# Create the interactive 3D plot
fig = px.scatter_3d(df, x='PC1', y='PC2', z='PC3', color=color_col, symbol=color_col, text=color_col,
labels={'PC1': 'Principal Component 1', 'PC2': 'Principal Component 2', 'PC3': 'Principal Component 3'})
# Customize the plot appearance
fig.update_layout(
margin=dict(l=0, r=0, t=0, b=0),
scene=dict(
xaxis_title='Principal Component 1',
yaxis_title='Principal Component 2',
zaxis_title='Principal Component 3',
),
)
# Show the plot
#fig.show()
pio.write_html(fig, file="3d_pca_plot.html", auto_open=True)
files.download("3d_pca_plot.html")
return fig
fig = plot_3d_pca(X_test, y_test, ['0','1','2','3','4','5','6','7','8','9'])
11.8. Coding#
Problem 1: Change the hidden layer activation Function to be a ReLU
Hint:
Forward pass
# Hidden layer z_h = np.dot(x, self.weight_h.T) + self.bias_h a_h = np.maximum(0, z_h) # ReLU activation
Backward pass
d_a_h__d_z_h = a_h * (1 - a_h) is replaced with d_a_h__d_z_h = np.where(a_h > 0, 1, 0).
This applies the derivative of ReLU, which is 1 when a_h > 0 and 0 when a_h <= 0.
##########################
### MODEL
##########################
def sigmoid(z):
return 1. / (1. + np.exp(-z))
def int_to_onehot(y, num_labels):
ary = np.zeros((y.shape[0], num_labels)) # [n_examples, n_classes]
for i, val in enumerate(y):
ary[i, val] = 1
return ary
class InitializeModel:
def __init__(self, random_seed=123):
print("Model initialization")
self.random_seed = random_seed
# Set up a common random number generator
self.rng = np.random.RandomState(random_seed)
# Common attribute for all models
self.operation = "Initialization"
class NeuralNetMLP_ReLU(InitializeModel):
def __init__(self, num_features, num_hidden, num_classes, random_seed=123):
super().__init__(random_seed)
"""
self.num_classes = num_classes
# hidden
#rng = np.random.RandomState(random_seed)
self.weight_h = self.rng.normal(
loc=0.0, scale=0.1, size=(num_hidden, num_features))
self.bias_h = np.zeros(num_hidden)
# output
self.weight_out = self.rng.normal(
loc=0.0, scale=0.1, size=(num_classes, num_hidden))
self.bias_out = np.zeros(num_classes)
"""
self.num_classes = num_classes
self.num_features = num_features
self.num_hidden = num_hidden
self._initialize_weights()
def _initialize_weights(self):
"""Initialize weights and biases with random values."""
# Initialize hidden layer weights and biases
self.weight_h = self.rng.normal(
loc=0.0, scale=0.1, size=(self.num_hidden, self.num_features))
self.bias_h = np.zeros(self.num_hidden)
# Initialize output layer weights and biases
self.weight_out = self.rng.normal(
loc=0.0, scale=0.1, size=(self.num_classes, self.num_hidden))
self.bias_out = np.zeros(self.num_classes)
def reinitialize(self, random_seed=None):
"""Reinitialize the model weights and biases if you need to."""
if random_seed is not None:
self.rng = np.random.RandomState(random_seed)
self._initialize_weights()
def forward(self, x):
# Hidden layer
# input dim: [n_examples, n_features] dot [n_hidden, n_features].T
# output dim: [n_examples, n_hidden]
z_h = np.dot(x, self.weight_h.T) + self.bias_h
a_h = np.maximum(0, z_h) # ReLU activation
# Output layer
# input dim: [n_examples, n_hidden] dot [n_classes, n_hidden].T
# output dim: [n_examples, n_classes]
z_out = np.dot(a_h, self.weight_out.T) + self.bias_out
a_out = sigmoid(z_out)
return a_h, a_out
def backward(self, x, a_h, a_out, y):
#########################
### Output layer weights
#########################
# onehot encoding
y_onehot = int_to_onehot(y, self.num_classes)
# For simplicity, the loss function is assumed to be the same we saw in Adaline, that is an MSE
# Loss = 1/n \sum_{i=1}^{n} 1/t \sum_{j=1}^{t} (y^{i}_{j}-outa^{i}_{j})^2
# Later on we will look at other loss functions such as multi-category cross-entropy loss
# Part 1: dLoss/dOutWeights
## = dLoss/dOutAct * dOutAct/dOutZ * dOutz/dOutWeight
## where DeltaOut = dLoss/dOutAct * dOutAct/dOutZ
## for convenient re-use
# input/output dim: [n_examples, n_classes]
d_loss__d_a_out = 2.*(a_out - y_onehot) / y.shape[0]
# input/output dim: [n_examples, n_classes]
d_a_out__d_z_out = a_out * (1. - a_out) # sigmoid derivative (<--- demonstrate)
# output dim: [n_examples, n_classes]
delta_out = d_loss__d_a_out * d_a_out__d_z_out # "delta (rule) placeholder"
# gradient for output weights
# [n_examples, n_hidden]
d_z_out__dw_out = a_h
# input dim: [n_classes, n_examples] dot [n_examples, n_hidden]
# output dim: [n_classes, n_hidden]
d_loss__dw_out = np.dot(delta_out.T, d_z_out__dw_out)
d_loss__db_out = np.sum(delta_out, axis=0) # [n_classes]
#################################
# Part 2: dLoss/dHiddenWeights
## = DeltaOut * dOutZ/dHiddenAct * dHiddenAct/dHiddenZ * dHiddenZ/dWeight
# [n_classes, n_hidden]
d_z_out__a_h = self.weight_out
# output dim: [n_examples, n_hidden]
d_loss__a_h = np.dot(delta_out, d_z_out__a_h)
# [n_examples, n_hidden]
d_a_h__d_z_h = np.where(a_h > 0, 1, 0)
# [n_examples, n_features]
d_z_h__d_w_h = x
# output dim: [n_hidden, n_features]
d_loss__d_w_h = np.dot((d_loss__a_h * d_a_h__d_z_h).T, d_z_h__d_w_h)
d_loss__d_b_h = np.sum((d_loss__a_h * d_a_h__d_z_h), axis=0)
return (d_loss__dw_out, d_loss__db_out,
d_loss__d_w_h, d_loss__d_b_h)
#********************************************************#
#****************** THE MODEL *********************#
#********************************************************#
model_relu = NeuralNetMLP_ReLU(num_features=28*28,
num_hidden=50,
num_classes=10)
#********************************************************#
#********************************************************#
#********************************************************#
Model initialization
np.random.seed(123) # for the training set shuffling
#model.reinitialize()
epoch_loss, epoch_train_acc, epoch_valid_acc = train(
model_relu, X_train, y_train, X_valid, y_valid,
num_epochs=40, learning_rate=0.1)
Epoch: 001/040 | Train MSE: 0.0206 | Train Acc: 88.81% | Valid Acc: 88.84%
Epoch: 002/040 | Train MSE: 0.0163 | Train Acc: 90.78% | Valid Acc: 90.74%
Epoch: 003/040 | Train MSE: 0.0143 | Train Acc: 91.97% | Valid Acc: 91.54%
Epoch: 004/040 | Train MSE: 0.0125 | Train Acc: 92.92% | Valid Acc: 92.72%
Epoch: 005/040 | Train MSE: 0.0117 | Train Acc: 93.40% | Valid Acc: 93.10%
Epoch: 006/040 | Train MSE: 0.0110 | Train Acc: 93.83% | Valid Acc: 93.26%
Epoch: 007/040 | Train MSE: 0.0103 | Train Acc: 94.36% | Valid Acc: 93.94%
Epoch: 008/040 | Train MSE: 0.0098 | Train Acc: 94.52% | Valid Acc: 94.08%
Epoch: 009/040 | Train MSE: 0.0091 | Train Acc: 94.91% | Valid Acc: 94.50%
Epoch: 010/040 | Train MSE: 0.0089 | Train Acc: 95.09% | Valid Acc: 94.74%
Epoch: 011/040 | Train MSE: 0.0085 | Train Acc: 95.40% | Valid Acc: 94.82%
Epoch: 012/040 | Train MSE: 0.0083 | Train Acc: 95.44% | Valid Acc: 94.82%
Epoch: 013/040 | Train MSE: 0.0078 | Train Acc: 95.75% | Valid Acc: 95.16%
Epoch: 014/040 | Train MSE: 0.0079 | Train Acc: 95.81% | Valid Acc: 95.28%
Epoch: 015/040 | Train MSE: 0.0075 | Train Acc: 95.92% | Valid Acc: 95.22%
Epoch: 016/040 | Train MSE: 0.0074 | Train Acc: 96.02% | Valid Acc: 95.30%
Epoch: 017/040 | Train MSE: 0.0070 | Train Acc: 96.21% | Valid Acc: 95.50%
Epoch: 018/040 | Train MSE: 0.0070 | Train Acc: 96.26% | Valid Acc: 95.54%
Epoch: 019/040 | Train MSE: 0.0069 | Train Acc: 96.26% | Valid Acc: 95.24%
Epoch: 020/040 | Train MSE: 0.0069 | Train Acc: 96.39% | Valid Acc: 95.72%
Epoch: 021/040 | Train MSE: 0.0063 | Train Acc: 96.62% | Valid Acc: 95.66%
Epoch: 022/040 | Train MSE: 0.0062 | Train Acc: 96.68% | Valid Acc: 95.80%
Epoch: 023/040 | Train MSE: 0.0061 | Train Acc: 96.80% | Valid Acc: 95.74%
Epoch: 024/040 | Train MSE: 0.0061 | Train Acc: 96.72% | Valid Acc: 95.74%
Epoch: 025/040 | Train MSE: 0.0059 | Train Acc: 96.87% | Valid Acc: 96.08%
Epoch: 026/040 | Train MSE: 0.0060 | Train Acc: 96.87% | Valid Acc: 95.88%
Epoch: 027/040 | Train MSE: 0.0057 | Train Acc: 96.94% | Valid Acc: 96.00%
Epoch: 028/040 | Train MSE: 0.0054 | Train Acc: 97.12% | Valid Acc: 96.14%
Epoch: 029/040 | Train MSE: 0.0054 | Train Acc: 97.06% | Valid Acc: 96.14%
Epoch: 030/040 | Train MSE: 0.0055 | Train Acc: 97.10% | Valid Acc: 96.20%
Epoch: 031/040 | Train MSE: 0.0052 | Train Acc: 97.21% | Valid Acc: 96.10%
Epoch: 032/040 | Train MSE: 0.0053 | Train Acc: 97.13% | Valid Acc: 96.04%
Epoch: 033/040 | Train MSE: 0.0052 | Train Acc: 97.20% | Valid Acc: 96.18%
Epoch: 034/040 | Train MSE: 0.0050 | Train Acc: 97.32% | Valid Acc: 96.26%
Epoch: 035/040 | Train MSE: 0.0050 | Train Acc: 97.33% | Valid Acc: 96.22%
Epoch: 036/040 | Train MSE: 0.0049 | Train Acc: 97.40% | Valid Acc: 96.18%
Epoch: 037/040 | Train MSE: 0.0048 | Train Acc: 97.41% | Valid Acc: 96.38%
Epoch: 038/040 | Train MSE: 0.0048 | Train Acc: 97.47% | Valid Acc: 96.34%
Epoch: 039/040 | Train MSE: 0.0047 | Train Acc: 97.50% | Valid Acc: 96.22%
Epoch: 040/040 | Train MSE: 0.0048 | Train Acc: 97.44% | Valid Acc: 96.30%
test_mse, test_acc = compute_mse_and_acc(model_relu, X_test, y_test)
print(f'Test accuracy: {test_acc*100:.2f}%')
Test accuracy: 96.09%