Implementing a GNN using the PyTorch Geometric library

27. Implementing a GNN using the PyTorch Geometric library#

!pip install torch torchvision torchaudio torch-geometric networkx matplotlib

Requirement already satisfied: torch in /usr/local/lib/python3.10/dist-packages (2.5.1+cu121)
Requirement already satisfied: torchvision in /usr/local/lib/python3.10/dist-packages (0.20.1+cu121)
Requirement already satisfied: torchaudio in /usr/local/lib/python3.10/dist-packages (2.5.1+cu121)
Collecting torch-geometric
  Downloading torch_geometric-2.6.1-py3-none-any.whl.metadata (63 kB)
     ━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━ 63.1/63.1 kB 1.4 MB/s eta 0:00:00
?25hRequirement already satisfied: networkx in /usr/local/lib/python3.10/dist-packages (3.4.2)
Requirement already satisfied: matplotlib in /usr/local/lib/python3.10/dist-packages (3.8.0)
Requirement already satisfied: filelock in /usr/local/lib/python3.10/dist-packages (from torch) (3.16.1)
Requirement already satisfied: typing-extensions>=4.8.0 in /usr/local/lib/python3.10/dist-packages (from torch) (4.12.2)
Requirement already satisfied: jinja2 in /usr/local/lib/python3.10/dist-packages (from torch) (3.1.4)
Requirement already satisfied: fsspec in /usr/local/lib/python3.10/dist-packages (from torch) (2024.10.0)
Requirement already satisfied: sympy==1.13.1 in /usr/local/lib/python3.10/dist-packages (from torch) (1.13.1)
Requirement already satisfied: mpmath<1.4,>=1.1.0 in /usr/local/lib/python3.10/dist-packages (from sympy==1.13.1->torch) (1.3.0)
Requirement already satisfied: numpy in /usr/local/lib/python3.10/dist-packages (from torchvision) (1.26.4)
Requirement already satisfied: pillow!=8.3.*,>=5.3.0 in /usr/local/lib/python3.10/dist-packages (from torchvision) (11.0.0)
Requirement already satisfied: aiohttp in /usr/local/lib/python3.10/dist-packages (from torch-geometric) (3.11.2)
Requirement already satisfied: psutil>=5.8.0 in /usr/local/lib/python3.10/dist-packages (from torch-geometric) (5.9.5)
Requirement already satisfied: pyparsing in /usr/local/lib/python3.10/dist-packages (from torch-geometric) (3.2.0)
Requirement already satisfied: requests in /usr/local/lib/python3.10/dist-packages (from torch-geometric) (2.32.3)
Requirement already satisfied: tqdm in /usr/local/lib/python3.10/dist-packages (from torch-geometric) (4.66.6)
Requirement already satisfied: contourpy>=1.0.1 in /usr/local/lib/python3.10/dist-packages (from matplotlib) (1.3.1)
Requirement already satisfied: cycler>=0.10 in /usr/local/lib/python3.10/dist-packages (from matplotlib) (0.12.1)
Requirement already satisfied: fonttools>=4.22.0 in /usr/local/lib/python3.10/dist-packages (from matplotlib) (4.55.0)
Requirement already satisfied: kiwisolver>=1.0.1 in /usr/local/lib/python3.10/dist-packages (from matplotlib) (1.4.7)
Requirement already satisfied: packaging>=20.0 in /usr/local/lib/python3.10/dist-packages (from matplotlib) (24.2)
Requirement already satisfied: python-dateutil>=2.7 in /usr/local/lib/python3.10/dist-packages (from matplotlib) (2.8.2)
Requirement already satisfied: six>=1.5 in /usr/local/lib/python3.10/dist-packages (from python-dateutil>=2.7->matplotlib) (1.16.0)
Requirement already satisfied: aiohappyeyeballs>=2.3.0 in /usr/local/lib/python3.10/dist-packages (from aiohttp->torch-geometric) (2.4.3)
Requirement already satisfied: aiosignal>=1.1.2 in /usr/local/lib/python3.10/dist-packages (from aiohttp->torch-geometric) (1.3.1)
Requirement already satisfied: attrs>=17.3.0 in /usr/local/lib/python3.10/dist-packages (from aiohttp->torch-geometric) (24.2.0)
Requirement already satisfied: frozenlist>=1.1.1 in /usr/local/lib/python3.10/dist-packages (from aiohttp->torch-geometric) (1.5.0)
Requirement already satisfied: multidict<7.0,>=4.5 in /usr/local/lib/python3.10/dist-packages (from aiohttp->torch-geometric) (6.1.0)
Requirement already satisfied: propcache>=0.2.0 in /usr/local/lib/python3.10/dist-packages (from aiohttp->torch-geometric) (0.2.0)
Requirement already satisfied: yarl<2.0,>=1.17.0 in /usr/local/lib/python3.10/dist-packages (from aiohttp->torch-geometric) (1.17.2)
Requirement already satisfied: async-timeout<6.0,>=4.0 in /usr/local/lib/python3.10/dist-packages (from aiohttp->torch-geometric) (4.0.3)
Requirement already satisfied: MarkupSafe>=2.0 in /usr/local/lib/python3.10/dist-packages (from jinja2->torch) (3.0.2)
Requirement already satisfied: charset-normalizer<4,>=2 in /usr/local/lib/python3.10/dist-packages (from requests->torch-geometric) (3.4.0)
Requirement already satisfied: idna<4,>=2.5 in /usr/local/lib/python3.10/dist-packages (from requests->torch-geometric) (3.10)
Requirement already satisfied: urllib3<3,>=1.21.1 in /usr/local/lib/python3.10/dist-packages (from requests->torch-geometric) (2.2.3)
Requirement already satisfied: certifi>=2017.4.17 in /usr/local/lib/python3.10/dist-packages (from requests->torch-geometric) (2024.8.30)
Downloading torch_geometric-2.6.1-py3-none-any.whl (1.1 MB)
   ━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━ 1.1/1.1 MB 7.4 MB/s eta 0:00:00
?25hInstalling collected packages: torch-geometric
Successfully installed torch-geometric-2.6.1

import torch
import torch.nn.functional as F
import torch.nn as nn


from torch_geometric.datasets import QM9
from torch_geometric.loader import DataLoader
from torch_geometric.nn import NNConv, global_add_pool

import numpy as np

dset = QM9('.')
len(dset)

Downloading https://data.pyg.org/datasets/qm9_v3.zip
Extracting ./raw/qm9_v3.zip
Processing...
Using a pre-processed version of the dataset. Please install 'rdkit' to alternatively process the raw data.
Done!

130831

27.1. QM9 Dataset#

The QM9 dataset is a widely-used benchmark dataset in computational chemistry and machine learning for molecular property prediction. It contains quantum mechanical calculations for 134,000+ small organic molecules composed of hydrogen (H), carbon ©, nitrogen (N), oxygen (O), and fluorine (F). The dataset is a valuable resource for training models to predict quantum chemical properties of molecules.

27.2. Data Structure in QM9#

Each molecule in the QM9 dataset is represented as a graph, where:

  • Nodes represent atoms (H, C, N, O, F).

  • Edges represent bonds between the atoms.

In PyTorch Geometric, the dataset is stored in a Data object, which contains the following attributes:

Attribute

Shape

Description

x

[num_atoms, num_features]

Node feature matrix describing properties of each atom.

edge_index

[2, num_edges]

Connectivity matrix defining which atoms are connected by bonds (source and target nodes).

edge_attr

[num_edges, num_features]

Edge feature matrix describing properties of the bonds (e.g., bond type, aromaticity, etc.).

y

[1, num_targets]

Molecular property vector containing 19 quantum mechanical properties for the molecule.

pos

[num_atoms, 3]

3D Cartesian coordinates (x, y, z) of each atom in the molecule.

z

[num_atoms]

Atomic numbers of the atoms (e.g., 1 for H, 6 for C).

idx

[1]

Index of the molecule in the dataset.

name

string

Name of the molecule (e.g., gdb_128), corresponding to its GDB identifier.

 
data = dset[124]
data

Data(x=[13, 11], edge_index=[2, 24], edge_attr=[24, 4], y=[1, 19], pos=[13, 3], idx=[1], name='gdb_128', z=[13])

27.3. Details of Each Attribute#

27.3.1. x (Node Features)#

  • The x matrix contains features describing each atom in the molecule.

  • Example features may include:

    • Atomic number (Z): Numerical identifier for the atom (e.g., H = 1, C = 6).

    • Hybridization state: sp, sp2, sp3, etc.

    • Formal charge: Charge on the atom.

    • Number of valence electrons: Total electrons available for bonding.

27.3.2. edge_index (Edge Connectivity)#

  • This is a sparse matrix in COO (Coordinate List) format that defines the connections (bonds) between atoms.

    • The first row contains the source nodes of the edges.

    • The second row contains the target nodes of the edges.

27.3.3. edge_attr (Edge Features)#

  • This matrix contains features describing each bond in the molecule.

  • Example features may include:

    • Bond type: Single, double, triple, aromatic.

    • Bond length: Distance between the connected atoms.

    • Aromaticity: Whether the bond is part of an aromatic ring.

27.3.4. y (Molecular Properties)#

  • The y attribute is a vector of 19 quantum mechanical properties for the molecule, computed using Density Functional Theory (DFT).

  • Examples of these properties include:

    • HOMO: Energy of the Highest Occupied Molecular Orbital.

    • LUMO: Energy of the Lowest Unoccupied Molecular Orbital.

    • Dipole moment: Measure of the separation of positive and negative charges in the molecule.

    • Atomization energy: Energy required to break a molecule into individual atoms.

    • Polarizability: Molecule’s ability to polarize in an electric field.

27.3.5. pos (3D Atomic Positions)#

  • The pos attribute contains the 3D Cartesian coordinates of each atom in the molecule.

  • These are crucial for tasks involving spatial and geometric properties, such as force fields or molecular dynamics.

27.3.6. z (Atomic Numbers)#

  • The z attribute stores the atomic numbers of the atoms in the molecule.

Atomic Number (Z)

Element

Symbol

1

Hydrogen

H

6

Carbon

C

7

Nitrogen

N

8

Oxygen

O

9

Fluorine

F

27.3.7. idx (Molecule Index)#

  • This is the unique index of the molecule in the dataset, useful for tracking or referencing specific molecules.

27.3.8. name (Molecule Name)#

  • The name corresponds to the GDB identifier of the molecule (e.g., gdb_128 this is ethanol.).

# Lets visualize a few samples
import networkx as nx
from torch_geometric.utils import to_networkx

# Convert the PyTorch Geometric graph to a NetworkX graph
G = to_networkx(data, node_attrs=['x'], edge_attrs=None)

# Inspect the graph
print(G.nodes(data=True))
print(G.edges(data=True))

[(0, {'x': [0.0, 1.0, 0.0, 0.0, 0.0, 6.0, 0.0, 0.0, 0.0, 0.0, 3.0]}), (1, {'x': [0.0, 1.0, 0.0, 0.0, 0.0, 6.0, 0.0, 0.0, 0.0, 0.0, 2.0]}), (2, {'x': [0.0, 1.0, 0.0, 0.0, 0.0, 6.0, 0.0, 0.0, 0.0, 0.0, 2.0]}), (3, {'x': [0.0, 1.0, 0.0, 0.0, 0.0, 6.0, 0.0, 0.0, 0.0, 0.0, 1.0]}), (4, {'x': [0.0, 0.0, 0.0, 1.0, 0.0, 8.0, 0.0, 0.0, 0.0, 0.0, 0.0]}), (5, {'x': [1.0, 0.0, 0.0, 0.0, 0.0, 1.0, 0.0, 0.0, 0.0, 0.0, 0.0]}), (6, {'x': [1.0, 0.0, 0.0, 0.0, 0.0, 1.0, 0.0, 0.0, 0.0, 0.0, 0.0]}), (7, {'x': [1.0, 0.0, 0.0, 0.0, 0.0, 1.0, 0.0, 0.0, 0.0, 0.0, 0.0]}), (8, {'x': [1.0, 0.0, 0.0, 0.0, 0.0, 1.0, 0.0, 0.0, 0.0, 0.0, 0.0]}), (9, {'x': [1.0, 0.0, 0.0, 0.0, 0.0, 1.0, 0.0, 0.0, 0.0, 0.0, 0.0]}), (10, {'x': [1.0, 0.0, 0.0, 0.0, 0.0, 1.0, 0.0, 0.0, 0.0, 0.0, 0.0]}), (11, {'x': [1.0, 0.0, 0.0, 0.0, 0.0, 1.0, 0.0, 0.0, 0.0, 0.0, 0.0]}), (12, {'x': [1.0, 0.0, 0.0, 0.0, 0.0, 1.0, 0.0, 0.0, 0.0, 0.0, 0.0]})]
[(0, 1, {}), (0, 5, {}), (0, 6, {}), (0, 7, {}), (1, 0, {}), (1, 2, {}), (1, 8, {}), (1, 9, {}), (2, 1, {}), (2, 3, {}), (2, 10, {}), (2, 11, {}), (3, 2, {}), (3, 4, {}), (3, 12, {}), (4, 3, {}), (5, 0, {}), (6, 0, {}), (7, 0, {}), (8, 1, {}), (9, 1, {}), (10, 2, {}), (11, 2, {}), (12, 3, {})]

from torch_geometric.utils import to_networkx
import matplotlib.pyplot as plt
import networkx as nx

# Mapping atomic numbers to elements and colors
atomic_number_to_element = {1: 'H', 6: 'C', 7: 'N', 8: 'O', 9: 'F'}
atomic_number_to_color = {1: 'blue', 6: 'green', 7: 'red', 8: 'yellow', 9: 'purple'}

# Convert PyTorch Geometric graph to NetworkX
G = to_networkx(data)

# Extract atomic numbers and corresponding elements/colors
atomic_numbers = data.x[:, 5].tolist()  # Assuming column 5 contains atomic numbers
elements = [atomic_number_to_element[int(z)] for z in atomic_numbers]
node_colors = [atomic_number_to_color[int(z)] for z in atomic_numbers]

# Create a legend
legend_elements = [
    plt.Line2D([0], [0], marker='o', color='w', markerfacecolor=color, markersize=10, label=atomic_number_to_element[element])
    for element, color in atomic_number_to_color.items()
]

# Node labels using element symbols
node_labels = {i: elements[i] for i in range(len(elements))}

# Plot the graph
plt.figure(figsize=(8, 6))
nx.draw(
    G,
    with_labels=True,
    node_color=node_colors,
    edge_color='gray',
    node_size=500,
    font_size=10,
)

# Add the legend
plt.legend(handles=legend_elements, loc='best', title="Atomic Elements")
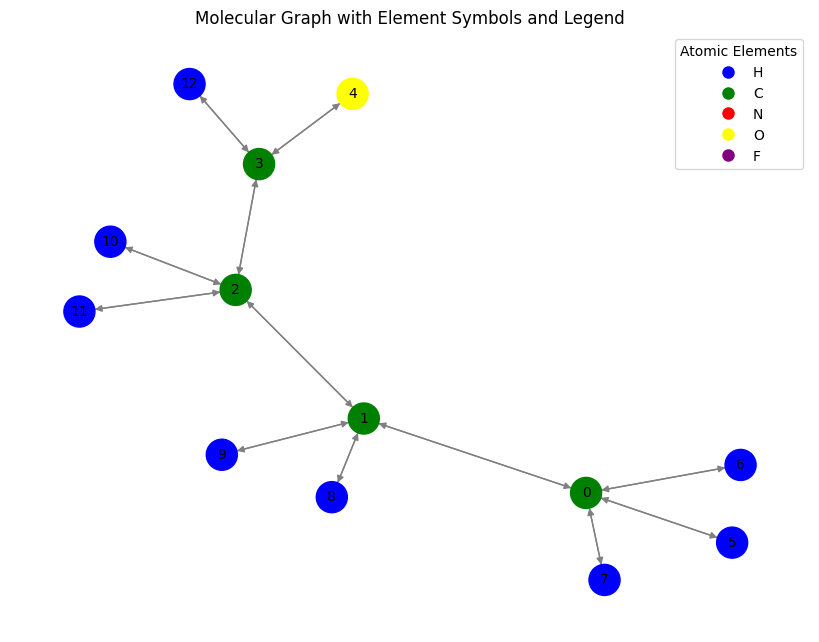
plt.title("Molecular Graph with Element Symbols and Legend")
plt.show()
_images/bdc68565c3a9cabd203a44a0be6e1dba2bb7fdb24d8e48af9226f8be99961782.png 
# New information can be added as

data.new_attribute = torch.tensor([1, 2, 3])
data

Data(x=[5, 11], edge_index=[2, 8], edge_attr=[8, 4], y=[1, 19], pos=[5, 3], idx=[1], name='gdb_1', z=[5], new_attribute=[3])

device = torch.device("cuda:0" if torch.cuda.is_available() else "cpu")
data.to(device)
data.new_attribute.is_cuda

True

class ExampleNet(torch.nn.Module):
    def __init__(self,num_node_features,num_edge_features):
        super().__init__()
        conv1_net = nn.Sequential(nn.Linear(num_edge_features, 32),
                                  nn.ReLU(),
                                  nn.Linear(32, num_node_features*32))
        conv2_net = nn.Sequential(nn.Linear(num_edge_features,32),
                                  nn.ReLU(),
                                  nn.Linear(32, 32*16))
        self.conv1 = NNConv(num_node_features, 32, conv1_net)
        self.conv2 = NNConv(32, 16, conv2_net)
        self.fc_1 = nn.Linear(16, 32)
        self.out = nn.Linear(32, 1)

    def forward(self, data):
        batch, x, edge_index, edge_attr=data.batch, data.x, data.edge_index, data.edge_attr
        x = F.relu(self.conv1(x, edge_index, edge_attr))
        x = F.relu(self.conv2(x, edge_index, edge_attr))
        x = global_add_pool(x,batch)
        x = F.relu(self.fc_1(x))
        output = self.out(x)
        return output

from torch.utils.data import random_split


train_set, valid_set, test_set = random_split(dset,[110000, 10831, 10000])

trainloader = DataLoader(train_set, batch_size=32, shuffle=True)
validloader = DataLoader(valid_set, batch_size=32, shuffle=True)
testloader = DataLoader(test_set, batch_size=32, shuffle=True)

qm9_node_feats, qm9_edge_feats = 11, 4
epochs = 4
net = ExampleNet(qm9_node_feats, qm9_edge_feats)

optimizer = torch.optim.Adam(net.parameters(), lr=0.01)
epochs = 4
target_idx = 1 # index position of the polarizability label

device = torch.device("cuda:0" if torch.cuda.is_available() else "cpu")
net.to(device)

ExampleNet(
  (conv1): NNConv(11, 32, aggr=add, nn=Sequential(
    (0): Linear(in_features=4, out_features=32, bias=True)
    (1): ReLU()
    (2): Linear(in_features=32, out_features=352, bias=True)
  ))
  (conv2): NNConv(32, 16, aggr=add, nn=Sequential(
    (0): Linear(in_features=4, out_features=32, bias=True)
    (1): ReLU()
    (2): Linear(in_features=32, out_features=512, bias=True)
  ))
  (fc_1): Linear(in_features=16, out_features=32, bias=True)
  (out): Linear(in_features=32, out_features=1, bias=True)
)

for total_epochs in range(epochs):

    epoch_loss = 0
    total_graphs = 0
    net.train()
    for batch in trainloader:
        batch.to(device)
        optimizer.zero_grad()
        output = net(batch)
        loss = F.mse_loss(output, batch.y[:, target_idx].unsqueeze(1))
        loss.backward()
        epoch_loss += loss.item()
        total_graphs += batch.num_graphs
        optimizer.step()

    train_avg_loss = epoch_loss / total_graphs
    val_loss = 0
    total_graphs = 0
    net.eval()
    for batch in validloader:
        batch.to(device)
        output = net(batch)
        loss = F.mse_loss(output,batch.y[:, target_idx].unsqueeze(1))
        val_loss += loss.item()
        total_graphs += batch.num_graphs
    val_avg_loss = val_loss / total_graphs


    print(f"Epochs: {total_epochs} | epoch avg. loss: {train_avg_loss:.2f} | validation avg. loss: {val_avg_loss:.2f}")

Epochs: 0 | epoch avg. loss: 0.42 | validation avg. loss: 0.15
Epochs: 1 | epoch avg. loss: 0.14 | validation avg. loss: 0.14
Epochs: 2 | epoch avg. loss: 0.11 | validation avg. loss: 0.08
Epochs: 3 | epoch avg. loss: 0.10 | validation avg. loss: 0.19

net.eval()
predictions = []
real = []

for batch in testloader:

    output = net(batch.to(device))
    predictions.append(output.detach().cpu().numpy())
    real.append(batch.y[:, target_idx].detach().cpu().numpy())

predictions = np.concatenate(predictions)
real = np.concatenate(real)

import matplotlib.pyplot as plt


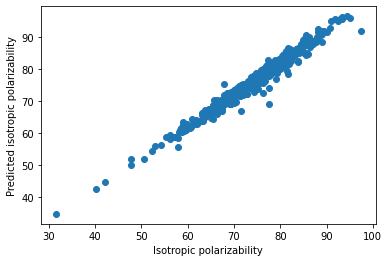
plt.scatter(real[:500],predictions[:500])
plt.ylabel('Predicted isotropic polarizability')
plt.xlabel('Isotropic polarizability')
#plt.savefig('figures/18_12.png', dpi=300)

Text(0.5, 0, 'Isotropic polarizability')
_images/8835fd2f68acfaa6f24792ad7436c25de1484dd4f6259ba822250a7e8c6daddc.png

27.4. Pointers to advanced graph neural network literature#

Contents