Bayesian Polynomial Regression
Contents
Bayesian Polynomial Regression#
import numpy as np
import arviz as az
import matplotlib.pyplot as plt
import requests
import io
import csv
import pandas as pd
target_url = 'https://raw.githubusercontent.com/cfteach/brds/main/datasets/anscombe.csv'
download = requests.get(target_url).content
ans = pd.read_csv(io.StringIO(download.decode('utf-8')))
x = ans[ans.group == 'II']['x'].values
y = ans[ans.group == 'II']['y'].values
x = x - x.mean()
f=plt.figure()
f.set_figwidth(4)
f.set_figheight(2)
plt.xlabel('x')
plt.ylabel('y')
plt.plot(x,y,'C0.',alpha=0.6, markersize=20)
#!pip install pymc3
import pymc3 as pm
with pm.Model() as model_poly:
alpha = pm.Normal('alpha',mu=y.mean(),sigma=1)
beta1 = pm.Normal('beta1',mu=0.,sigma=1)
beta2 = pm.Normal('beta2',mu=0.,sigma=1)
epsilon = pm.HalfCauchy('epsilon', 5)
mu = pm.Deterministic('mu',alpha + beta1*x + beta2*x*x)
y_pred = pm.Normal('y_pred', mu=mu, sigma = epsilon, observed = y)
trace_poly = pm.sample(2000, tune = 2000, return_inferencedata=True)
az.plot_trace(trace_poly, var_names = ['alpha','beta1','beta2'])
res = az.summary(trace_poly)
print(res)
tr_alpha = res.loc['alpha']
tr_beta1 = res.loc['beta1']
tr_beta2 = res.loc['beta2']
print(tr_alpha)
alpha_m = tr_alpha['mean']
beta1_m = tr_beta1['mean']
beta2_m = tr_beta2['mean']
xr = np.linspace(-6,6,100)
yr = alpha_m + beta1_m*xr + beta2_m*xr**2
f = plt.figure(figsize=(10,5))
plt.plot(xr,yr, c='C1')
plt.plot(x,y, 'C0.')
Perturbed Dataset#
Let’s modify the previous dataset by introducing some noise
#print(y)
#tidx = int(np.floor(len(y)/2))
#print(tidx)
#print(y[0])
#print(type(y))
yn = y.copy()
#tidx = 0
#yn[tidx] = yn[tidx] + np.random.normal(0,2.)
yn += np.random.normal(0,.5, len(yn))
f = plt.figure(figsize=(7,3))
plt.plot(x,yn,'C0.')
plt.plot(xr,yr,'--')
---------------------------------------------------------------------------
NameError Traceback (most recent call last)
Cell In [6], line 16
14 f = plt.figure(figsize=(7,3))
15 plt.plot(x,yn,'C0.')
---> 16 plt.plot(xr,yr,'--')
NameError: name 'xr' is not defined

with pm.Model() as model_poly2:
alpha = pm.Normal('alpha',mu=y.mean(),sigma=1)
beta1 = pm.Normal('beta1',mu=0.,sigma=1)
beta2 = pm.Normal('beta2',mu=0.,sigma=1)
epsilon = pm.HalfCauchy('epsilon', 5)
mu = pm.Deterministic('mu',alpha + beta1*x + beta2*x*x)
y_pred_per = pm.Normal('y_pred_per', mu=mu, sigma = epsilon, observed = yn)
trace_poly_per = pm.sample(2000, tune = 2000, return_inferencedata=True)
Auto-assigning NUTS sampler...
Initializing NUTS using jitter+adapt_diag...
Multiprocess sampling (4 chains in 4 jobs)
NUTS: [epsilon, beta2, beta1, alpha]
100.00% [16000/16000 00:02<00:00 Sampling 4 chains, 2 divergences]
/Users/cfanelli/Desktop/teaching/BRDS/jupynb_env_new/lib/python3.9/site-packages/scipy/stats/_continuous_distns.py:624: RuntimeWarning: overflow encountered in _beta_ppf
return _boost._beta_ppf(q, a, b)
/Users/cfanelli/Desktop/teaching/BRDS/jupynb_env_new/lib/python3.9/site-packages/scipy/stats/_continuous_distns.py:624: RuntimeWarning: overflow encountered in _beta_ppf
return _boost._beta_ppf(q, a, b)
/Users/cfanelli/Desktop/teaching/BRDS/jupynb_env_new/lib/python3.9/site-packages/scipy/stats/_continuous_distns.py:624: RuntimeWarning: overflow encountered in _beta_ppf
return _boost._beta_ppf(q, a, b)
/Users/cfanelli/Desktop/teaching/BRDS/jupynb_env_new/lib/python3.9/site-packages/scipy/stats/_continuous_distns.py:624: RuntimeWarning: overflow encountered in _beta_ppf
return _boost._beta_ppf(q, a, b)
Sampling 4 chains for 2_000 tune and 2_000 draw iterations (8_000 + 8_000 draws total) took 9 seconds.
There were 2 divergences after tuning. Increase `target_accept` or reparameterize.
az.plot_trace(trace_poly_per)
array([[<AxesSubplot:title={'center':'alpha'}>,
<AxesSubplot:title={'center':'alpha'}>],
[<AxesSubplot:title={'center':'beta1'}>,
<AxesSubplot:title={'center':'beta1'}>],
[<AxesSubplot:title={'center':'beta2'}>,
<AxesSubplot:title={'center':'beta2'}>],
[<AxesSubplot:title={'center':'epsilon'}>,
<AxesSubplot:title={'center':'epsilon'}>],
[<AxesSubplot:title={'center':'mu'}>,
<AxesSubplot:title={'center':'mu'}>]], dtype=object)
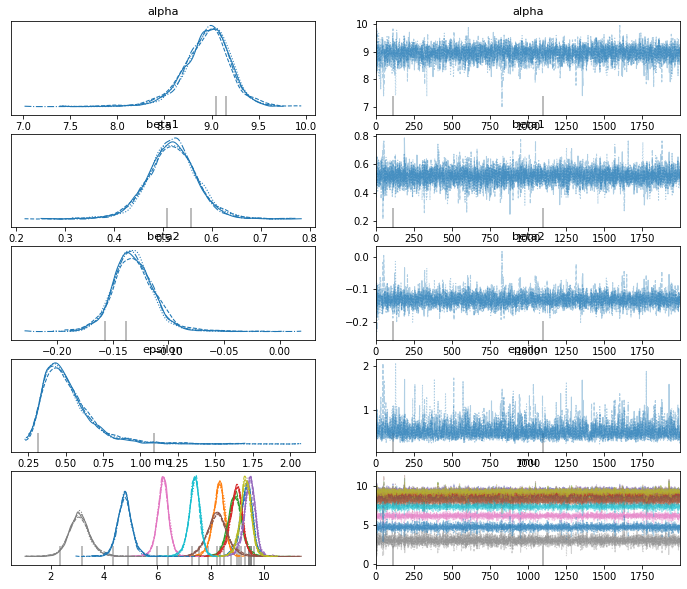
res2 = az.summary(trace_poly_per)
print(res2)
mean sd hdi_3% hdi_97% mcse_mean mcse_sd ess_bulk \
alpha 8.949 0.253 8.461 9.406 0.005 0.003 3571.0
beta1 0.519 0.052 0.421 0.617 0.001 0.001 4749.0
beta2 -0.131 0.019 -0.167 -0.096 0.000 0.000 3844.0
epsilon 0.512 0.172 0.266 0.809 0.003 0.002 2723.0
mu[0] 9.337 0.245 8.887 9.811 0.004 0.003 3739.0
mu[1] 8.299 0.245 7.849 8.758 0.004 0.003 3670.0
mu[2] 8.921 0.288 8.379 9.446 0.004 0.003 5672.0
mu[3] 8.949 0.253 8.461 9.406 0.005 0.003 3571.0
mu[4] 9.461 0.227 8.989 9.835 0.004 0.003 4315.0
mu[5] 8.257 0.417 7.461 9.034 0.006 0.004 4876.0
mu[6] 6.209 0.228 5.778 6.625 0.003 0.002 5577.0
mu[7] 3.067 0.419 2.272 3.846 0.006 0.004 5730.0
mu[8] 9.323 0.228 8.886 9.741 0.003 0.002 5540.0
mu[9] 7.385 0.227 6.961 7.797 0.004 0.003 4205.0
mu[10] 4.770 0.289 4.207 5.293 0.004 0.003 6466.0
ess_tail r_hat
alpha 2957.0 1.0
beta1 3561.0 1.0
beta2 2975.0 1.0
epsilon 3095.0 1.0
mu[0] 3240.0 1.0
mu[1] 3097.0 1.0
mu[2] 4263.0 1.0
mu[3] 2957.0 1.0
mu[4] 4379.0 1.0
mu[5] 3778.0 1.0
mu[6] 4135.0 1.0
mu[7] 4661.0 1.0
mu[8] 4726.0 1.0
mu[9] 3310.0 1.0
mu[10] 4960.0 1.0
#az.plot_hdi(x,res2['mu'], color='k')
ppc = pm.sample_posterior_predictive(trace_poly_per, samples=4000, model=model_poly2)
/Users/cfanelli/Desktop/teaching/BRDS/jupynb_env_new/lib/python3.9/site-packages/pymc3/sampling.py:1708: UserWarning: samples parameter is smaller than nchains times ndraws, some draws and/or chains may not be represented in the returned posterior predictive sample
warnings.warn(
100.00% [4000/4000 00:01<00:00]
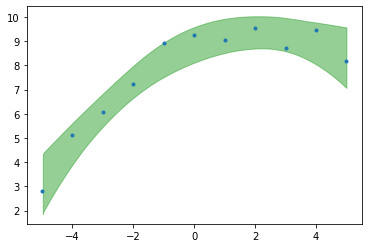
plt.plot(x,yn,'C0.')
az.plot_hdi(x,trace_poly_per.posterior['mu'],color='C2',hdi_prob=.99)
<AxesSubplot:>